当初私は、自分の推理に何かつまらない間違いがあるにちがいないと考えた。私は推理の各手順（ひとつひとつのステップ）を、論理的顕微鏡（under a logical microscope）で詳しく点検した。しかし、間違いを何も発見できなかった。私はこのことについて、フレーゲ（Friedrich Ludwig Gottlob Frege, 1848- 1925：ドイツの論理学者、数学者で、数理論理学の祖）に手紙を書いた。彼の返事には、算術がよろめき始めており、また、自分の(『算術の基本法則』の)第五法則は間違っていることがわかった、と書かれていた。フレーゲはこの矛盾（ラッセルのパラドクス）によって、非常に落胆させられ、算術を論理学から演繹する企て －それまで自分の生涯の主な目標としていたもの－ を断念した。通約不可能性（注：incommensurables 共約不可能性。体系、概念、方法論などに違いを持つ異なる体系（パラダイム）同士の間で、概念間の対応付けがうまく出来ない状態のこと）（という難物）に直面したピタゴラス学派の人々のように、フレーゲは幾何学の中へ逃避し、どうやら（apparently）それまでの自分の生涯の仕事は見当違いであったと考えたらしい。私はどうかといえば、困難の原因（trouble）は数学の中によりもむしろ論理学の中にあり、改めらるぺきは論理学の方であると感じた。私は、厳密に無限数の矛盾をつくり出すことのできる方法の発見によって、この見解（の正しさ）を確信した。

Chapter 7: Principia Mathematica: Philosophical Aspects, n.4
At first I thought there must be some trivial error in my reasoning. I inspected each step under a logical microscope, but I could not discover anything wrong. I wrote to Frege about it, who replied that arithmetic was tottering and that he saw that his Law V was false. Frege was so disturbed by this contradiction that he gave up the attempt to deduce arithmetic from logic, to which, until then, his life had been mainly devoted. Like the Pythagoreans when confronted with incommensurables, he took refuge in geometry and apparently considered that his life’s work up to that moment had been misguided. For my part, I felt that the trouble lay in logic rather than in mathematics and that it was logic which would have to be reformed. I was confirmed in this view by discovering a recipe by means of which a strictly infinite number of contradictions could be manufactured.
　Source: My Philosophical Development, chap. 7：1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_07-040.HTM

（発展の方向の）不愉快な側面は、疑いもなくとても不愉快なものであった。（即ち、）学派の区別なく,全ての論理学者が、アリストテレスの時代以来ずっと受け入れてきた前提から、（いろいろな）矛盾が演繹され（導出され）、何かがまちがっていることを示しているがしかしどそれらの問題をどうやって正したらよいかについては何も示していないように思われた。私が享受しつつあった論理的蜜月（logical honeymoon）を終わらせたのは、1901年の春に、そういう矛盾のびとつを私が発見したことであった（注：これが論理学史上有名な「ラッセルのパラドクス」の発見）。私はこの不幸をホワイトヘッドに伝えた彼は「喜びに満ち自信が溢れる朝は再び来らず（never glad confident morning again 喜ばしい確固とした朝は二度と来ないのだ！）」という句を引いて私をなぐさめようとしたが、無駄であった。 　私がこの矛盾に導かれたのは、最大の基数（cardinal number）は存在しないというカントールの証明を吟味することによってであった。私は、無邪気にも、世界にある全てのものの数（総数）は最大の数であるに違いないと信じ、カントールの証明をこの数に適用し、どういう結果が出てくるかを見ようとした。このプロセス（手順/処置）は、非常に奇妙な集合の考察へと私を導いた。それまで正しいと思っていたやり方で考えを進めてゆくと、一つの集合が、ある時は自己自身（その集合自身）の要素（成員/メンバー）でありかつ（同時に）自己自身の要素でないようにと思われた。たとえばティースプーン（紅茶やコーヒー用のスプーン）の集合は、ティースプーン（自体）ではない。しかしティースプーンでないものの集合は、ティースプーンでない集合(one)のひとつである。さらにこのように否定的なものではないところの例も存在すると思われた。たとえば、全ての集合の集合は、ひとつの集合である。ところでカントールの議論（論証）を適用していって、私は、「自己自身の要素でない諸集合」を考えるに至ったが、これらの集合もまたひとつの集合を形づくらなければならないと思われた。そこで私は、この集合がそれ自身の要素であるかないか、自問した。もしそれがそれ自身の要素であるならば、それは、その集合の定義をなしている特性、すなわち、それ自身の要素でないという特性をもたらざるを得ない。逆にもしそれがそれ自身の要素でないとするなら、それはその集合の定義をつくっている特性をもってはならないのだから、それは、それ自身の要素でなければならない。このようにして、二つの可能性のいずれをとっても、それは自身の反対に導き、従って矛盾に陥ることになる。

Chapter 7: Principia Mathematica: Philosophical Aspects, n.3 The unpleasant aspect was indubitably very unpleasant. It appeared that, from premisses which all logicians of no matter what school had accepted ever since the time of Aristotle, contradictions could be deduced, showing that something was amiss but giving no indication as to how matters were to be put right. It was the discovery of one such contradiction, in the spring of 1901 , that put an end to the logical honeymoon that I had been enjoying. I communicated the misfortune to Whitehead, who failed to console me by quoting, ‘never glad confident morning again’. I was led to this contradiction by considering Cantor’s proof that there is no greatest cardinal number. I thought, in my innocence, that the number of all the things there are in the world must be the greatest possible number, and I applied his proof to this number to see what would happen. This process led me to the consideration of a very peculiar class. Thinking along the lines which had hitherto seemed adequate, it seemed to me that a class sometimes is, and sometimes is not, a member of itself. The class of teaspoons, for example, is not another teaspoon, but the class of things that are not teaspoons, is one of the things that are not teaspoons. There seemed to be instances which are not negative: for example, the class of all classes is a class. The application of Cantor’s argument led me to consider the classes that are not members of themselves; and these, it seemed, must form a class. I asked myself whether this class is a member of itself or not. If it is a member of itself, it must possess the defining property of the class, which is to be not a member of itself. If it is not a member of itself, it must not possess the defining property of the class, and therefore must be a member of itself. Thus each alternative leads to its opposite and there is a contradiction.
　Source: My Philosophical Development, chap. 7：1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_07-030.HTM

『プリンキピア・マテマティカ(数学原理)』の第一の目標（目的）は、純粋数学の全体が純粋に論理学的な前提から帰結し（導出し）かつ、（それは）論理的名辞（logical terms 論理項）によって定義される概念のみを用いる、ということを示すことにあった。これは、もちろん、カントの学説に反対の主張であった。ゲオルグ・カントールは、カントを「あの理屈をこねるフェリシテ人（門外漢／俗物／教養のない者）」と呼び、さらに意味をはっきりさせるために「数学をほとんど知らないところの」とつけ加えたが、私は当初この研究（『プリンキピア・マテマティカ』の執筆）を、カントに対する反駁につけられる一つの付加的説明(as a parenthesis)だと考えていた。しかし時が経つにつれ、この研究（仕事）は二つの異なる方向に発展していった。（即ち）数学的側面においては、全く新たな主題(whole new subjects)が明るみになり（came to light）、新たなアルゴリズム（数学的な問題を解くための一連の手順）を必要とし、それはそれまで冗長で不正確な日常言語にゆだねられていた諸問題を、記号的にとり扱うことを可能にした（のである）。哲学的側面においては、二つの反対（方向）－ひとつは嬉しい、もうひとつは嬉しくない－ 発展があった。嬉しい方向というのは、その仕事（研究）に必要とする論理的装置が、私が以前予想していたよりも小さいものだと判明したことであった。とりわけ、集合（classes）という概念が不要であることがわかったことであった。（私の前著の）『数学の諸原理』においては、一（個）として見られた集合と、多（数）として見られた集合との区別について、多くの議論が存在していた。けれどもこの議論の全体は、この本(前著)に含まれた多くの複雑な（こみ入った）議論と共に、不要であることがわかった(のである)。その結果、『プリンキピア・マテマティカ（数学原理）』は、その最終形においては、不明瞭ということを最も容易に目立つ特徴とするところの哲学的深遠さなるものを欠いているように一見みえたのである（注：非常に明晰なものとなった、ということ／「曖昧に書けば深遠に見える」と感じる人への皮肉）。

Chapter 7: Principia Mathematica: Philosophical Aspects, n.2 The primary aim of Principia Mathematica was to show that all pure mathematics follows from purely logical premisses and uses only concepts definable in logical terms. This was, of course, an antithesis to the doctrines of Kant, and initially I thought of the work as a parenthesis in the refutation of ‘yonder sophistical Philistine’, as Georg Cantor described him, adding for the sake of further definiteness, ‘who knew so little mathematics’. But as time went on, the work developed in two different directions. On the mathematical side, whole new subjects came to light, involving new algorithms making possible the symbolic treatment of matters previously left to the diffuseness and inaccuracy of ordinary language. On the philosophical side, there were two opposite developments, one pleasant and the other unpleasant. The pleasant one was that the logical apparatus required turned out to be smaller than I had supposed. More especially, classes turned out to be unnecessary. In The Principles of Mathematics there is a lot of discussion about the distinction between a class as one and a class as many. The whole of this discussion, along with a great many complicated arguments contained in that book, proved unnecessary. The consequence was that the work in its final form appeared to lack that philosophic profundity of which obscurity is the most easily recognizable feature.
　Source: My Philosophical Development, chap. 7：1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_07-020.HTM

　1900年から1910年までの間ずっと、ホワイトヘッドと私の二人は、我々の時間のほとんど（bulk of 大部分）を、最終的に『プリンキピア・マテマティカ（数学原理）』(Principia Mathematica)となったもの（仕事）に費やした。この著作の第３巻は、1913年まで出版されなかったが（1913年にようやく出版されたが）、この本を書く仕事は － 校正刷読みは別として－ 1910年に全ての原稿を私達がケンブリッジ大学出版部にもって行った時に終っていた。(これより先)1902年5月23日に書きあげた『数学の諸原理』(The Principles of Mathematics)は、後の著作（『プリンキピア・マテマティカ』の粗雑かなり未熟な下書きであることがわかったけれども、それは後の本（『プリンキピア・マテマティカ』）とはちがって、他の（自分とは立場や考え方が異なる）数理哲学（数学の哲学）との論争を含んでいた。 　我々が論争しなければならない問題は二種類、即ち、哲学的問題と数学的問題の２つがあった。大雑把に言うと、ホワイトヘッドは哲学的問題を私に任せた。数学的問題については、ホワイトヘッドがその記法（notation 記号法）の大部分を、ペアノ（が考案したもの）から借りたものは別として、考案した。（数学的問題については）私は系列(series)に関する仕事の大部分をやり、ホワイトヘッドはそれ以外の大部分をやった。しかしこれは初稿についてのみあてはまる（applies to そうである／該当する）。各部とも、三度書き直された。我々二人のどちらかが初稿を書きあげる、それを相手に送ると、受け取った方はかなり修正を行う（行った）。それが終ると、初稿を書いた方が、決定版（最終稿）に書き直した。三巻全体にわたって、二人の協同の成果（産物）でないものはほとんど一行も存在していない。
Chapter 7: Principia Mathematica: Philosophical Aspects, n.1 Throughout the years from 1900 to 1910 both Whitehead and I gave the bulk of our time to what ultimately became Principia Mathematica, Although the third volume of this work was not published until 1913, our part in it (apart from proof-reading) was finished in 1910 when we took the whole manuscript to the Cambridge University Press. The Principles of Mathematics which I finished on May 23, 1902, turned out to be a crude and rather immature draft of the subsequent work, from which, however, it differed in containing controversy with other philosophies of mathematics. The problems with which we had to contend were of two sorts: philosophical and mathematical. Broadly speaking, Whitehead left the philosophical problems to me. As for the mathematical problems, Whitehead invented most of the notation, except in so far as it was taken over from Peano; I did most of the work concerned with series and Whitehead did most of the rest. But this only applies to first drafts. Every part was done three times over. When one of us had produced a first draft, he would send it to the other, who would usually modify it considerably .After which, the one who had made the first draft would put it into final form. There is hardly a line in all the three volumes which is not a joint product.
　Source: My Philosophical Development, chap. 7：1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_07-010.HTM

　私が既に言及した事柄に加えて、ペアノとその弟子たちの仕事のなかで（in the work 仕事において）私を喜ばせた点は他にもいろいろあった。私は彼らが図形(figures)を用いないで幾何学を展開し、そうして（thus 結果として/従って）カントの（言う）直観(Anschauung)が必要ないことを明示しているやり方を好んだ。また私は（一つの平面積の）全領域を満たすペアノの曲線(curve)を好んだ（注：ウィキペディアに「ペアノ曲線」に関する説明がありますので、興味のある方はお読みください）。しかし、ペアノに出会う前は、私は関係（というもの）の重要性を痛感していたので、ペアノに会うとすぐに(all at once)、関係の論理を記号的に扱うことによって、彼（ペアノ）の仕事を補う作業にとりかかった。私がベアノに会ったのは(1900年)７月末であり、私が彼が編集している雑誌に発表した関係の論理についての論文を執筆したのは９月であった。私は同じ年の10月、11月、12月を『数学の諸原理』（The Principles of Mathematics）に執筆に費やした。（出版された）この本の第３，４、５，６の各章は、この３ケ月の間に私が書いたほとんどそのままのものである。けれども、第１，２，７章は後に書き直した。私は『数学の諸原理』の初稿を19世紀の最後の日、つまり1900年12月31日に書きあげた。その年の７月以降の月々は、私がそれ以前にもそれ以後にも決して経験したことのないような知的蜜月（intellectual honeymoon）であった。私は毎日、前日まで理解していなかったことを理解している自分を発見した。私は（数学の原理に関する）あらゆる困難が取り除かれ、あらゆる問題が片づいたと思った。しかし、知的蜜月は続かず、翌年（1901年）の始めには、知的な悲しみが私にたっぷり（in full measure）ふりかかってきた。
Chapter 6: Logical Technique in Mathematics, n.10
In addition to the matters that I have already mentioned, there were other things that delighted me in the work of Peano and his disciples. I liked the way in which they developed geometry without the use of figures, thus displaying the needlessness of Kant’s Anschauung and I liked Peano’s curve that filled a whole area. But before coming across Peano I had been filled with the importance of relations, and I therefore set to work almost at once supplementing what he had done by a symbolic treatment of the logic of relations. It was at the end of July that I met him, and it was in September that I wrote a paper on the logic of relations which was published in his journal. I spent October, November and December of that same year on The Principles of Mathematics, Parts III, IV, V and VI of that book are almost exactly as I wrote them during those months. Parts I, II and VII, however, I re-wrote later. I finished this first draft of The Principles of Mathematics on the last day of the nineteenth century – i.e. December 31, 1900. The months since the previous July had been an intellectual honeymoon such as I have never experienced before or since. Every day I found myself understanding something that I had not understood on the previous day. I thought all difficulties were solved and all problems were at an end. But the honeymoon could not last, and early in the following year intellectual sorrow descended upon me in full measure. 　
　Source: My Philosophical Development, chap. 6：1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_06-100.HTM

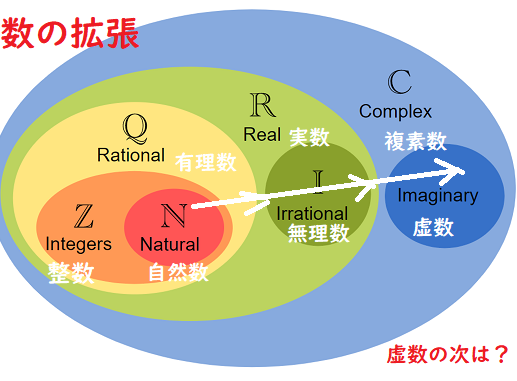
　上記のように整数（whole numbers）を定義すれは、数学が必要とする(数の)拡張（注：整数→分数→有理数→無理数→実数→虚数→複素数といった拡張のこと）には何の困難も存在しない（まったく困難はない）。(即ち)有理分数（rational fractions 分母・分子ともが有理数あるいは多項式である分数）とは、整数の間の関係で,乗法（掛け算）に由来するものである。（注：分数 n/m は割り算 n ÷ m の商、あるいは単位分数 1/mのn倍の数と捉えることができる。／みすず書房版の訳書で、野田又夫氏は「rational fractions」を「分数」と訳しているが、「二つの整数の間の関係」と書いているのであるから、分母あるいは分子に無理数がくる分数は除かなければならない。）実数とは、0からある点までの間に存在する全ての有理数の集合である。たとえば、2の平方根とは、その平方が2よりも小さい全ての有理数である。この定義をはじめて発見したのは私であったと思うが、この定義はピタゴラスの時代以来、数学者を悩まし続けてきた難問を片づけてしまう。複素数（注：実数の単位1と，i2(二乗) ＝－1 であるような虚数単位 i との2つの単位によって構成される数。任意の複素数 z は，a，b を実数として z ＝ a ＋ bi の形に書かれる）は、実数の対（つい）とみなすことができ、このとき、対という語の意味の中には、第一項と第二項があるという意味、即ち,それ（その対）においては項の順序が絶対不可欠であるという意味、が含まれている。
Chapter 6: Logical Technique in Mathematics, n.9
Having defined the whole numbers as above, there is no difficulty in the extensions that mathematics requires. Rational fractions are relations between whole numbers which are derived from multiplication. Real numbers are sets of rational numbers consisting of everything above zero until a certain point. For example, the square-root of two is all rational numbers whose square is less than two. This definition, of which I believe I was the inventor, puts an end to a puzzle which had perplexed mathematicians ever since the time of Pythagoras. Complex numbers can be regarded as couples of real numbers, using ‘couple’ in the sense in which there is a first term and a second term – i.e. in which the order of the terms is essential.
　Source: My Philosophical Development, chap. 6：1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_06-090.HTM

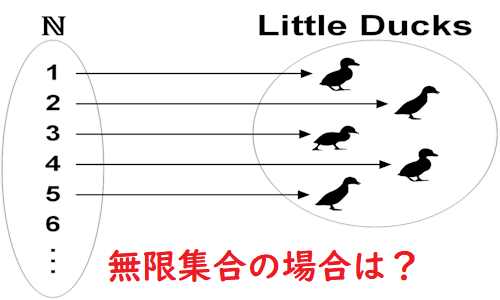
上記の数の定義（法）は、きわめて重要な、さらなるもうひとつの利点を提供する。その利点というのは、無限数に関する多くの困難（問題）に終止符を打つということ（利点）である。項（terms）を一つずつ取りあげて数えることから数が得られると考えられていた間は(While numbers were derived from counting …)、一度に一つずつとって（one at a time）枚挙しつくことのできないような集合の（要素である）数を思い描くことは困難であった。たとえば，我々は、数えることによって、有限数（finite numbers）の終り（最後の数）に到達することは不可能である。どれほど数え続けても、常にそれより大きな数が存在している。それゆえ、数は数えることから生ずると考えられていた間は、有限数が（最大）いくつあるかについて語ることは不可能であると思われた。けれども、今や、数えることはある一つの集合の中にどれだけ多くの項があるかを見出すための単なる一つの方法にすぎず、それはたまたま（数が）有限であるような集合にのみ適用しうるものであるこように思われる。数えることのロジック（論理）を、新しい学説に適合するように考え直すと、次のようになる。たとえば、いまポンド紙幣（pound notes）を数えているとしてみよう。意志行為によって（act of will 無意識にではなく意志をもって）、我々は数枚の紙幣と、数 l、2、3等々との間に、一対一の関係をつけ、もう残った紙幣がないところまで対応付けを行う。そうすると(then)上記の我々の定義（法）に従い（in accordance with）、紙幣の数は、あなたが言及してきた数の数（number of numbers）と同一であることがわかる（注：1,2,3,4,5と5まで数えてもう紙幣が残っていなければ「５」がその数になるということ）。そして、もし我々は１から数え始めて、どの数をもスキップしないで進んだのであれば、言及した数の数は、最後に挙げた数である（注：数え方はいろいろあるためにこのように言っている）。このやり方を、無限集合に適用することはできない。なぜなら、我々の生命はそれほど長くないからである。しかし数えるということはもはや絶対に必須ではないので、そのことはまったく気にする必要はない。（that need cause you no concern）

Chapter 6: Logical Technique in Mathematics, n.8
The above definition of numbers offers a further advantage which is of profound importance, and that is that it puts an end to difficulties concerning infinite numbers. While numbers were derived from counting, which takes terms one by one, it was difficult to conceive of the numbers of collections which could not be exhaustively enumerated one at a time. You cannot, for example, come to an end of the finite numbers by counting: however long you go on, there are always larger numbers to come. Therefore, so long as numbers were derived from counting, it seemed impossible to speak of the number of finite numbers. Now, however, it appears that counting is only one way of discovering how many terms there are in a collection, and is only applicable to such collections as happen to be finite. The logic of counting, as fitted into the new theory, is as follows: suppose, for example, that you are counting pound notes. By an act of will, you establish a one-one relation between the several notes and the numbers 1, 2, 3, etc., until there are no notes left. You then know, in accordance with our definition, that the number of notes is the same as the number of numbers that you have mentioned, and, if you have begun with 1 and gone on without skipping, the number of numbers that you have mentioned is the last number that you have mentioned. You cannot apply this process to infinite collections because life is not long enough. But, as counting is no longer essential, that need cause you no concern.
　Source: My Philosophical Development, chap. 6：1959． 　　　　
　More info.:https://russell-j.com/beginner/BR_MPD_06-080.HTM

　この定義(の仕方)は、種々の利点(advantages)がある。それは、以前、0と1とについて生じていた問題全てを片づけてしまう（deals with 処理する）。(即ち，この定義によれば) 0とは、要素をもたない集合の集合である。つまり、それは（0とは）その唯一の要素が、要素をまったく持たない（一つの）集合であるところの集合である。1とは、ある項 x と同一である任意の項からなるという特性（属性）を持つ集合の集合である。(この定義法の)第二の利点は、一と多に関する困難を乗り越える（gets over）という点である。数えられる項は、一つの命題関数の例（instances 事例）として数えられるので、それに伴う（含まれる）統一性(the unity involved)は、もっぱら「命題関数（として）統一性であり、それは決して例(事例)の多数性とは衝突（矛盾）しない。しかし、これら二つの利点のいずれよりも重要なのは、我々が形而上学的存在者としての数を排除できるということである。数は，実際、単なる言語上の便利なもの（便宜的なもの）にすぎないものとなり、「その他/等々」（etc）とか つまり/即ち（i.e）とかいう略字のもつ以上の実体性を持つものではなくなる。クロネッカー(注：1823-1891、ドイツの数学者)は、数学について哲学的思索を行い、「神が整数をつくり、数学者がその他の数学的道具立てをつくった」と言った。彼が言おうとしたのは、全ての整数は独立の存在者でなければならないが、他の種類の数は独立した存在である必要（性）はない、ということであった。(しかし)上に述べた数の定義（法）により、整数の持つこのような特権は消滅し、数学者の基本的な道具立て（primitive 基本の，根本の）は、「あるいは（or）」とか「ない（not)」とか「全ての（all）」とか「ある（some）」とかいうような純粋に論理的な名辞（論理項）に還元されるのである（減少させられる）。これが、一定の知識の体系において、未定義の術語（terms）及び証明されていない命題の数を減らすために、オッカムの剃刀がいかに有用であるか、ということについての私の最初の経験であった。
Chapter 6: Logical Technique in Mathematics, n.7
This definition has various advantages. It deals with all the problems that had previously arisen concerning 0 and 1. 0 is the class of those classes that have no members – i.e. it is the class whose only member is a class having no members. 1 is the class of those classes that have the property of consisting of whatever is identical with some term x, A second advantage of the definition is that it gets over difficulties concerning the one and the many. Since the terms counted are counted as instances of a propositional function, the unity involved is only that of the propositional function, which in no way conflicts with the plurality of instances. But much more important than either of these two advantages is the fact that we get rid of numbers as metaphysical entities. They become, in fact, merely linguistic conveniences with no more substantiality than belongs to ‘etc.’ or ‘i.e.’. Kronecker, in philosophizing about mathematics, said that ‘God made the integers and the mathematicians made the rest of the mathematical apparatus’. By this he meant that each integer had to have an independent being, but other kinds of numbers need not have. With the above definition of numbers this prerogative of the integers disappears and the primitive apparatus of the mathematician is reduced to such purely logical terms as or, not, all and some. This was my first experience of the usefulness of Occam’s razor in diminishing the number of undefined terms and unproved propositions required in a given body of knowledge.
　Source: My Philosophical Development, chap. 6：1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_06-070.HTM

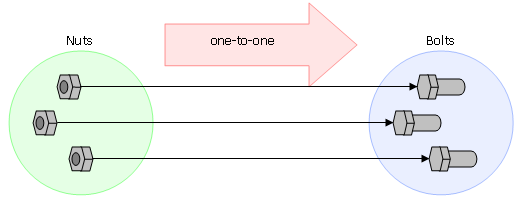
　数についての（ペアノ）以前の理論は、0と1とについて、常に困難に陥った（陥っていた）。そして、まず私が感心したのは、これらの困難を扱うペアノの手腕であった。しかし、この新しい観点の全帰結を私が引き出したのはそれからかなり経ってからのことであった。数学において（は）「集合」（classs）について考えることは便利であり（であるので）、長い間私は集合と命題関数とを区別する必要があると考えていた。けれども、最終的にはこの区別が技術的工夫として以外には不必要であるとの結論に達した。「命題関数」という句は、多分、不必要に恐ろしげに（formidable）聞こえるかも知れない。多くの場合、それは「特性（属性）」（property）という語で言いかえることが可能である。その結果として（thus それゆえ）我々は、各々の数は諸特性のなかの一特性（a property of certain properties）であると言ってよいであろうが、しかし、最終的な分析における場合以外は、「集合」(class)という語を使い続けることが、いっそう容易であろう。 　上記の考察によって私が導かれた数の定義は、それよりも16年も早く（前に）、フレーゲによって定式化されていた（はっきりと述べられていたが、私はそのことを、私がそれを再発見したおよそ一年後まで知らなかった。私は（数の）２を「あらゆる対（couple つい）の集合」と定義し、(数の）３を「あらゆる三つ組（trio）の集合」等々、と定義した。「対」というのは、xとyという要素をもつ集合であって、xとyとは同一でなく、かつもし第三者zがその集合の要素であるなら、zはxかyのいずれかと同一であるような集合である。一般に一つの数とは、「類似性（相似性）」（similarity）と言われる特性（属性）をもつところの,集合の集合(a set of classes)である。「類似性（相似性）」は次のように定義される。即ち、二つの集合はそれらの諸項（terms）を一つずつ対(つい)にする方法がある（存在する）とき、類似的（相似）であると言われる。たとえば、一夫一婦制の国においては(in a monogamous country)、結婚している男の数は結婚している女の数と同数であるということを、男女がそれぞれ何人いるかを知らずとも、知ることが可能である（注：現代では結婚が男女の組み合わせ以外もあるようになったため、このように断言できなくなっている）。（私は夫を失った妻や妻を失った夫を勘定に入れていない。）　さらにまた、一人の人が片足を失っていないなら、彼のもっている右足の靴の数は、左足の靴の数と同じであることはかなりの場合確かであろう。また、ある会の出席者が皆椅子に坐っており、かつ空いた椅子が一つもなければ、椅子の数は椅子に坐っている人間の数と同じに違いない。これらすべての場合において、一方の集合の要素と他方の集合の要素との間に、いわゆる一対一の関係が存在するのであり、そういう一対一の関係の存在こそ「類似性」といわれるものである。そこで任意の集合の数とは、その集合に類似な集合の全てであると定義される。

Chapter 6: Logical Technique in Mathematics, n.6 The older theories of number always got into difficulties over 0 and 1, and it was Peano’s capacity of dealing with these difficulties that first impressed me. But it was a good many years before I drew the full consequences of the new point of view. It is convenient in mathematics to think of ‘classes’, and for a long time I thought it necessary to distinguish between classes and propositional functions. Ultimately, however, I came to the conclusion that this distinction is unnecessary except as a technical device. The phrase ‘propositional function’ sounds perhaps unnecessarily formidable. For many purposes one can substitute the word ‘property’. Thus, we may say that each number is a property of certain properties, but, except in ultimate analysis, it is perhaps easier to continue to use the word ‘class’. The definition of numbers to which I was led by the above considerations had been formulated by Frege sixteen years earlier, but I did not know this until a year or so after I had re-discovered it. I defined 2 as the class of all couples, 3 as the class of all trios, etc. A couple is defined as a class of which there are members x and y, x is not identical with y, and, if z is a member of the class, then z is identical with x or with y, A number, in general, is a set of classes having the property which is called ‘similarity’. This is defined as follows; Two classes are similar if there is a way of coupling their terms one to one. For example, in a monogamous country, you can know that the number of married men is the same as the number of married women, without having to know how many there are of either (I am excluding widows and widowers). Again, if a man has not lost a leg, you may be pretty sure that the number of his right-hand shoes is the same as the number of his left-hand shoes. If every member of a company has a chair to sit on and there are no empty chairs, the number of chairs must be the same as the number of people sitting on them. In all these cases there is what is called a one-one relation between the terms of one class and the terms of another, and it is the existence of such a one-one relation which is defined as similarity. The number of any class is defined as all the classes that are similar to it. 　
　Source: My Philosophical Development, chap. 6：1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_06-060.HTM

　算術の哲学は、フレーゲ以前のすべての著者によって間違って考えられていた。彼らの全てが犯した誤まりはとても自然なものであった。彼らは数を数えることによって生ずるものであると考えた。しかし、一（ひとつ）として数えられるものは、同様に多（数）としても同様に（equally well 負けず劣らず）数えられるゆえに、絶望的な困難に陥った。たとえば、イングランドにどれだけのフットボール・クラブ（注：英国ではサッカー・クラブのこと）があるか？という問いをとりあげてみよう。この間いに答える際、我々は各クラブを１つ（１チーム）としてとり扱う。しかしある一つのフットボール・クラブがどれだけの会員をもつかと問うことも同様に質問してもよいであろう（may just as well）。その場合には、我々はそのクラブを（部分を持たない一つのものではなく）多として扱っている。また（さらに）Ａ氏がこれらのクラブの中の一つに属する会員である場合、彼はそれ以前には１（人）として数えられているが、今度は、そのＡ氏がどれだけの数の分子から成っているか、と同様に正当に問うことが可能であろう（問うてもいいだろう）。そうして、その場合には、Ａ氏は多として数えられる（ことになる）。こういうわけで、数える際に何ものかを１たらしめるものは、そのものの物理的性質ではなく、「これは何の一例であるか？(Of what is this an instance?)」という問いなのである（注：人間の例としてなら一人、分子の例としてなら多数、となる）。数えることによって、我々が到達する数は、何らかの集合の数であり、その集合は我々がそれを（その要素/成員）数える前にどのような数であれ数を持っているのである（注：数えなくても人間なら一人、目の数なら２個、背骨の数は◯◯個、・・・等々）。集合が多であるのは、ただ何らかのものの多数の例としてである。そしてその集合自身（それ全体を一つとして考えた場合）はまた何か他の（別の）ものの例でありうるのであり、その例としては 一（つ）として数えられる（in enumeration 列挙すると、数えると）。このようにして，我々は「集合とは何か？」，また，「例とは何か？」という問いに対峙することを強いられる。この二つの問いはいずれも、命題関数（函数）という方法（手段）を用いないでは理解することができない。命題関数（函数）というのは、一つの変項を含む式(an expression 数式や論理式)であり、その変項に一つの値が指定される（割り当てられる）やいなや、一つの命題となるものである。たとえば、「xは人間である」は、一つの命題函数である。そして x の代りにソクラテスやプラトンやその他の誰かを置くと、我々は命題を得るのである。我々はまた，xを、人でないところのもので置きかえることもでき、そしてそれでもやはり（still）一つの命題を得るが、その場合には偽なる命題を得るわけである（注：たとえば、自宅の犬のポチを代入すると、「愛犬のポチは人間である」という偽命題ができる）。命題関数（函数）とは、一つの式（注：an expression 数式や論理式／因みに、みすず書房刊の野田訳では「表現」と訳出されている。）にすぎない。それは、それだけでは何ものをも表さない。しかし，それは、真偽いずれにせよ，何ものかを主張する文の一部を形作ることが可能である。「xは使徒であった」は、何ごとも意味しないが、「xは使徒であった』を真ならしめるような値が12ある（注：１２使徒のこと）」というのは完全（完璧）な文である。同様な考察（similar consideration）が、例（実例）という概念にも当てはまる。我々が何ものかを一つの例と見るとき、我々はそれをある命題関数の変項のもちうる一つの値と考えている。たとえば「ソクラテスは人間の一例である」と私が言うとき、私はソクラテスが、「x は人間である」を真にするxの一つの値である、ということを意味している。(中世の)スコラ哲学者は「一」（One）と「存在」（being）とは交換可能な名辞(terms)であるという趣旨の（to the effect that）格率（a maxim）を立てていた。この格率は、それが信ぜられているかぎり、(数の）１を定義することを不可能にした。実を言えば、「存在」は無用な（役に立たない）語であり、この無用な語が間違った仕方であるものに適用されると、それは一であるとともに多である，ということになりがちである。一は一つの特性（特質）であるが、それはもの（物）の特性（特質）ではなく、ある種の命題関数（函数）、つまり、次のような特性（特質）をもつ命題関数（函数）の特性（特質）である。（即ち）その関数を真にするxがあり、しかも、もしyがその関数を真にするならば、y は x と同一である、という特性（特質）である。これがただ一つの値をもつ関数（unitary function）の定義であり、数１はある種の関数がもつところの「ただ一つの値をもつ」（being unitary）という特性（特質）なのである。同様にして「空（くう）なる関数」（null-function）とは、xのあらゆる値に対して偽となる関数であり、0 とは「空なる関数である」という特性（特質）なのである。

Chapter 6: Logical Technique in Mathematics, n.5 The philosophy of arithmetic was wrongly conceived by every writer before Frege. The mistake that all of them made was a very natural one. They thought of numbers as resulting from counting, and got into hopeless puzzles because things that are counted as one can equally well be counted as many. Take, say, the question, ‘How many football clubs are there in England？’ In answering this question, you treat each club as one, but you may just as well ask: ‘How many members has such and such a football club.’ In that case, you treat the club as many. And, if Mr A is a member of one of these clubs, although he counted as one before, you may ask just as legitimately, ‘How many molecules make up Mr A?’ And, then, Mr A counts as many. It is obvious, therefore, that what makes anything one from the point of view of counting is not its physical constitution but the question, ‘Of what is this an instance?’ The number that you arrive at by counting is the number of some collection, and the collection has whatever number it does have before you count it. It is only qua many instances of something that the collection is many. The collection itself will be an instance of something else, and qua instance counts as one in enumeration. We are thus forced to face the question, ‘What is a collection?’ and ‘What is an instance?’ Neither of these is intelligible except by means of propositional functions. A propositional function is an expression containing a variable and becoming a proposition as soon as a value is assigned to the variable. For example, ‘x is a man’ is a propositional function. If, in place of x, we put Socrates or Plato or anybody else, we get a proposition. We can also replace x by something that is not a man and we still get a proposition, though in this case a false one. A propositional function is nothing but an expression. It does not, by itself, represent anything. But it can form part of a sentence which does say something, true or false: ‘x was an Apostle’ says nothing, but ‘there are twelve values of x for which “x was an Apostle” is true’ is a complete sentence. Similar considerations apply to the concept instance. When we consider something as an instance, we are considering it as a possible value of a variable in a propositional function. If I say, ‘Socrates is an instance of Man’ I mean Socrates is a value of x for which ‘x is a man’ is true. The Scholastics had a maxim to the effect that one and being are convertible terms. This maxim, so long as it was believed, made it impossible to define 1. The truth is that being is a useless word, and that the kind of things to which this useless word is applied by those who mistakenly use it are just as apt to be many as to be one. One is a characteristic, not of things, but of certain propositional functions, namely, of those propositional functions which have the following property: there is an x which makes the function true and which is such that, if y makes the function true, y is identical with x. This is the definition of unitary functions, and the number 1 is the property of being unitary which certain functions possess. Similarly, a null-function is one which is false for all values of x, and 0 is the property of being a null-function.
　Source: My Philosophical Development, chap. 6：1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_06-050.HTM