私が関心をもったもう一つの問題は、物質が空虚な空間によって切り離されている諸原子から成っているのか、それとも全空間（全宇宙）に広がるプレナム（注：”plenum”：物質が充満した空間）から成っているのか、という問題であった。当初，私は前者の見方に傾いていた。（注：現代物理学・宇宙論においても、宇宙において物質が占める割合はごくわずかであり、大部分はダーク・マターやダーク・エネルギーで占められていると主張されている。）この見方を最も論理的に述べた主唱者（exponent）はボスコヴィッチ（Boscovitch）であった。彼の見解によれば，一つの原子は空間の一点のみを占めるのであり、また（かつ）あらゆる（物質間の）相互作用は、ニュートンの万有引力の法則においてそうであるように、遠隔作用である。けれども，これとは異なる見解がファラデーの実験から生れており、電気と磁気に関するクラーク・マックスウェルの大著に具体的に示されていた。この著作はホワイトヘッドの給費研究員資格請求論文の主題となっていた。(原注：この理由により，ホワイトヘッドはケンブリッジでは，常に，純粋数学者であるよりもむしろ応用数学者であると見なされた。この見方は、ホワイトヘッドが『普遍的代数学』を書いたにも代わらず，『普遍的代数学』はそれが受けるに値するだけの注目をケンブリッジ大学は払わなかった。)　彼は私にボスコヴィッチの見方（見解）を捨ててこの見方（見解）をとるようにしきりに勧めた。この見解は、それを支持する経験的議論（論拠）をもっている上に、遠隔作用をなくす(仮定しなくてもよい)という長所も持っていた。遠隔作用は長い間、ニュートン自身にとってすらも、信じがたいものと思われていたものであった。より現代的なこの見方を採用した時、私はそれにヘーゲル風の衣裳をまとわせ、それをライプニッツからスピノザへの弁証法的移行として示し、そうして私が論理的順序と考えるものを、年代記の順序（時間順）に優先することを思い切って許したのである（注：年代の上ではスピノザの方がライプニッツより先／permit myself to allow）

Chapter 4: Excursion into Idealism, n.8
The other problem which concerned me was the question whether matter consists of atoms separated by empty space, or of a plenum pervading all space. I inclined at first to the former view, of which the most logical exponent was Boscovitch. According to his view, an atom occupies only a point of space, and all interaction is action at a distance, as in the Newtonian law of gravitation. A different view, however, had resulted from Faraday’s experiments and been embodied in Clerk Maxwell’s great book on electricity and magnetism. This book had been the subject of Whitehead’s Fellowship dissertation (* note), and Whitehead urged me to prefer its views to those of Boscovitch. In addition to empirical arguments in its favour, it had the advantage of doing away with action at a distance, which had always seemed incredible, even to Newton. When I adopted the more modern view, I gave it a Hegelian dress, and represented it as a dialectical transition from Leibniz to Spinoza, thus permitting myself to allow what I considered the logical order to prevail over that of chronology. (* Note: On this ground, Whitehead was always regarded at Cambridge as an applied, rather than a pure, mathematician. This view persisted in spite of Universal Algebra, to which Cambridge paid much less attention than it deserved.
　Source: My Philosophical Development, chap. 4,1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_04-080.HTM

　物理学の哲学において、二つの問題（問い）が特に私の興味をひいた。第一は絶対運動あるいは相対運動かの問題（問い）であった。ニュートンは（天体の）回転は当然絶対的なものであって相対的なものではない、ということを示す論証（argument)をしていた。この論証は人々を当惑させたが、人々はそれに十分に答える回答を見出しえなかったけれども、その反対の論証、即ちあらゆる運動は相対的であるという論証（議論）も、少なくともニュートンの論証（議論）と同程度に説得力がある（convincing）と思われた。そしてこの難問（puzzle 謎）はアインシュタインが彼の相対性理論を生み出すまで未解決のままであった。しかしヘーゲル弁証法の見地からは、それは二律背反（アンティノミー）の源泉（起源となるもの）として都合のよいものであった。物理学の中で解決を見出す必要はなく、ただ、物質が非実在的な抽象であり、物質に関するいかなる科学も論理的には満足すべきものではないということを認めれば足りる，と私はそのように（当時）考えていた（のである）。

Chapter 4: Excursion into Idealism, n.7
Two questions specially interested me in the philosophy of physics. The first of these was the question of absolute or relative motion. Newton had an argument to show that rotation must be absolute and not relative. But, although this argument worried people and they could not find an answer to it, the arguments for the contrary view, that all motion is relative, seemed at least equally convincing. This puzzle remained unsolved until Einstein produced his Theory of Relativity. From the point of view of Hegelian dialectics it was a convenient source of antinomies; it was not necessary (so I supposed) to find a solution within physics, but to acknowledge that matter is an unreal abstraction and that no science of matter can be logically satisfactory.
　Source: My Philosophical Development, chap. 4,1959． 　
More info.:https://russell-j.com/beginner/BR_MPD_04-070.HTM

　私は，若かった時　－－もしかすると現在でもそうかも知れないが－－　自分自身の理論が決定的に正しいものであること（finality 最終的なもの/決定的なもの）に対して、ほとんど信じられないほどの楽観主義（楽観的態度）を抱いていた。私は 幾何学の基礎に関する著書を1896年(注：ラッセル24歳）に書き終えると　－－幾何学に関する問題はもう片づけたという印象のもとに－－　ただちに、物理学も同様にとり扱う研究（仕事）へと進んだ。この物理学の基礎に関して２年間研究したが、当時の私の見解を示すものとして公けに発表したものは、既に言及した数と量に関する論文だけであった。当時の私はひとかど(full-fledged)のヘーゲル主義者であり、科学の弁証法の完全な体系を構築しようと目指しており、その体系は「あらゆる実在は精神的なもの（心的なもの）である」という証明によって完結すべきものであった。私は（当時）全ての科学は何らかの抽象化（abstraction 抽象的なもの）に依存しており、抽象化（抽象的なもの）は遅かれ早かれ（早晩）矛盾に導くものであるので、いかなる科学も完全な意味では真ではない、というヘーゲルの見解を受けいれていた。カントとヘーゲルとが対立する場合には,私はいつもヘーゲルに味方した。私はカントの　『自然科学の形而上学的原理』から強い印象を受け、それについて入念なメモを書いた。しかし，私はそのノートの中に次のように書いている、 「本書はカテゴリー表（範疇表）に対応して４つの部分に分けられており、各部（セクション）において、それぞれ３つの対応するカテゴリーに対して３つの法則が見出される。しかし,３つの法則は（というのは）通常はとても人為的である。２つの法則を立てるほうが自然であろう。」

Chapter 4: Excursion into Idealism, n.6
I had when I was younger — perhaps I still have — an almost unbelievable optimism as to the finality of my own theories. I finished my book on the foundations of geometry in 1896, and proceeded at once to what I intended as a similar treatment of the foundations of physics, being under the impression that problems concerning geometry had been disposed of. I worked on the foundations of physics for two years, but the only thing that I published expressing my views at that time was the article on number and quantity already mentioned. I was at this time a full-fledged Hegelian, and I aimed at constructing a complete dialectic of the sciences, which should end up with the proof that all reality is mental. I accepted the Hegelian view that none of the sciences is quite true, since all depend upon some abstraction, and every abstraction leads, sooner or later, to contradictions. Wherever Kant and Hegel were in conflict, I sided with Hegel. I was much impressed by Kant’s Metaphysische Anfangsgrunde der Naturwissenschaft and made elaborate notes on it, but I remarked, ‘the book is divided into four sections corresponding to the Table of Categories, and in each section three laws are found for the three corresponding categories. But the three laws are usually very artificial; two would be natural.’
　Source: My Philosophical Development, chap. 4,1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_04-060.HTM

　けれども、その後に続いたもの（ラッセルの論文）はもっとひどいものであった。私の幾何学に関する理論は主としてカント主義的であったが、その後，私はヘーゲル弁証法での取り組み（efforts）へと飛び込んでいった(plunged into)。「数と量との関係について」(注：1897年＝ﾗｯｾﾙ25歳の時の論文)という論文を書いたが、これは正真正銘の（unadulterated 混ぜ物のない）ヘーゲルである。この論文の要旨は、この論文の最初の二つの節に含まれており、それは以下の通りである。

　「私はこの論文で数理哲学における最も根本的な問題の一つを論じたい。微積分学（infinitesimal calculus）及びそのすべての帰結についての,要するに,高等数学全体についての,我々の解釈は、この関係（注：数と量との関係）について我々がいかなる見解を採るかに，依存していると言わなければならない。まさに連続の観念も －－ この観念は数学におけると同様哲学においても次第に人目を引くようになってきたものであり、特に近年、ヒユームとカントがともに持っていた原子論的見解をおしのけるにいたっている－－ 数学において数に対する量の意義が（相対的に）どの程度に認められるかにより（relative justification）、必然的に、左右されなければならない(stand or fall 成功するあるいは失敗する)と私は考える。けれども、ここでは数学的考察を行う必要はないだろう。数と量とを純粋に論理的な側面から考察することで十分であろう。私は,「量」という言葉を常に連続量と同等である（同じ意味をもつ）ものとして用いることにしよう。そしてこの論文において 連続的という語の意味を明瞭にすることに努めることにしよう。 　私の議論（論証）は以下のようになるであろう。最初に私は数を論じ（数について論じ）、正の整数（positive integers）を超えて数を拡張すること（注：負の整数、少数・・・）は、(数の)単位の特性をしだいに消滅させること（gradual absorbsion しだいに吸収すること）によって起るものであること、そうして,数の拡張は数全体に関する情報をしだいに減少させることを、私は示すであろう（shall show）(注：わかりにくいが、正の整数の場合は、１個、２個というように応用できる、負の整数の場合は借金として考えることができる。しかしそうした解釈も、分数、少数、虚数・・・となっていくと、この世の中に実例がある数として考えられなくなっていく、また、数とは何かということもわかりにくくなっていく、といったところだろうか？)。次に私は、数を連続体へ適用することを論じ(注：物を分割できて初めて数えることができる／たとえて言えば被連続体である数個の角砂糖と連続体であるコップ一杯の水)、数自体は量に関してまったく情報を与えず、既存の量的単位との比較を与えるのみであることを、示す（明らかにする）ことに努めることにしよう（注：これもわかりにくいが、小さなコップの中の水については水の分子の数のようなものを数えるなら数がでてくるが、通常は、数の概念は出てこない。しかし、小さなコップの正確に３倍の大きさのコップに水が入っているとすると、両者を比較すると、１：３という数がでてくる）。従って、量は単位の分析において探求されなければならない，と思われるだろう。量とはいろいろな量（的なもの）の固有の（本質的）ひとつの特性であると仮定し（Assuming quantity to be an intrinsic property of quantities）、私は（以下）２つの仮説について論ずることにしよう。第一の仮説は、量を他のものに還元することのできないカテゴリー（範疇）と見なすものであり、第二の仮説は、量を直接的な感覚的所与（センス・データ）と見なすものである。第一の仮説を採用する時、外延量（extensive quantity 「示強量」という訳語もあるがわかりにくい）がその分割可能性(を仮定すること)によって矛盾に陥ち、本当は分割できないものであり、それゆえ内包的なものとして受け取られなければならないことがわかるであろう(intensive 論理学用語で「内包的」。「内包」とは,ある概念がもつ共通な性質のこと。性質は分割できない。内包に対する言葉は「外延」。広がりのある外延は分割可能)。しかし,内包量（intensive quantity 「示容量」という訳語もあるがわかりにくい）が、もしいろいろな内包量の固有の一特性であるとしたら、内包量もまた,それらの諸特性の単なる関係にすぎないに違いない、と思われるであろう。従って,第一の仮説、即ち、量は一つの内包的特性を示すカテゴリー（範噂）であるという仮説は、斥けられねばならないことになるであろう。さて第二の仮説、すなわち量は感覚における所与（データ）であるという仮説もまた、矛盾に導くことが見出されるであろう。それゆえ、我々は量がいろいろな量の内包的特性であるという見解を斥けざるをえないであろう。（そこで）その代わりに、我々は量を比較のカテゴリー（範噂）の一つと見なそう。量的にとり扱うことができるものの間には、量的に比較できる質的に類似のものが存在するという、外面的な（外部的な）特性（extraneous property）のうちに含まれるものを除いて、共通の特性はまったく存在しない,と我々は言おう。このことは、量のカテゴリー（範疇）を、最も広い意味での，尺度（measure）のカテゴリー（範噂）に変えることであり、こうして前の多くの困難（問題）は消滅する，と私は考える。しかし同時に、量と数との全ての関係（conexion = connection）は消滅するであろう。（つまり）量、あるいは尺度は、数とは全く独立した比較（の）概念である、と我々は言うであろう。しかし、尺度（measure）のうちに含まれる比較の種類についての議論は、以前の困難（問題）を新たな形で再び呼び戻すであろう。比較される諸項は －－もはや量的なものとは見なされないが－－ やはり、この論文の最初の部分で量そのものに属するに属していたであろうものに類似した矛盾に感染している（陥っている）ことに気づくであろう。私は、量とは現実的ならびに可能的な直接の所与（データ）の集合にのみ適用可能であり，いかなる十分に理解される物質(?)（fully understood material）には適用されないものである、と私は結論する（結論を下すことにしよう）。」


　クーチェラ(Louis Couturat, 1868-1914:フランスの哲学者で論理学者)はこの論文のことを「精緻な弁証法の小さな傑作」（ce petit chef d’oeuvre de dialectique subtile）と言ってくれたが、今の私にとっては、全くとりえがないがらくたとしか思えない。

Chapter 4: Excursion into Idealism, n.5
However, there was worse to follow. My theory of geometry was mainly Kantian, but after this I plunged into efforts at Hegelian dialectic. I wrote a paper ‘On the Relations of Number and Quantity’ which is unadulterated Hegel. The gist of this paper is contained in its first two paragraphs, which are as follows: I wish in this paper to discuss one of the most fundamental questions of mathematical philosophy. On the view we take of this relation must depend our interpretation of the Infinitesimal Calculus and all its consequences — in a word, of all higher mathematics. The very idea of the continuum — an idea which, in philosophy as in mathematics, has become gradually more and more prominent, and has, of late especially, ousted the atomic views which were shared by Hume and Kant — must stand or fall, I think, with the relative justification of quantity in mathematics as against number. It will not be necessary, however, to deal with mathematical considerations here; it will be sufficient to consider number and quantity in their purely logical aspects. I shall use quantity, always, as equivalent to continuous quantity, and I shall endeavour, in the course of the paper, to make clear the meaning of the word continuous. My argument will be as follows: First, I shall discuss number, and show that its extensions beyond the positive integers result from a gradual absorption of the properties of the unit, and give a gradually diminishing information as to the whole. Then I shall discuss the application of number to continua, and shall endeavour to show that number per se gives no information as to quantity, but only comparison with an already quantitative unit. It will appear, therefore, that quantity must be sought in an analysis of the unit. Assuming quantity to be an intrinsic property of quantities, I shall discuss two hypotheses. The first regards quantity as an irreducible category, the second regards it as an immediate sense-datum. On the first hypothesis, we shall see that extensive quantities are rendered contradictory by their divisibility, and must be taken as really indivisible, and so intensive. But intensive quantity too, it will appear, must, if it be an intrinsic property of intensive quantities, be also a mere relation between them. The hypothesis that quantity is a category giving an intrinsic property will therefore have to be rejected. The hypothesis that quantity is a datum in sense will also be found to lead to contradictions. We shall be forced, therefore, to reject the view that quantity is an intrinsic property of quantities. We shall regard it, instead, as a category of comparison ; there is no common property, we shall say, among things that can be treated quantitatively, except what is involved in the extraneous property that there are other qualitatively similar things with which they can be quantitatively compared. This will turn quantity into measure, in the broadest sense, and with this, I think, our previous difficulties will cease. But at the same time, every connexion with number will cease — quantity or measure, we shall say, is a wholly independent conception of comparison. But a discussion of the kind of comparison involved in measure will bring back our previous difficulties in a new form; we shall find that the terms compared, though we no longer regard them as quantitative, are infected with contradictions similar to those which, in the first part of the paper, will have belonged to quantity itself. I shall conclude that quantity is only applicable to classes of actual and possible immediate data, and not to any fully understood material. Although Couturat described this article as ‘ce petit chef d’oeuvre de dialectique subtile’, it seems to me now nothing but unmitigated rubbish.
　Source: My Philosophical Development, chap. 4,1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_04-050.HTM

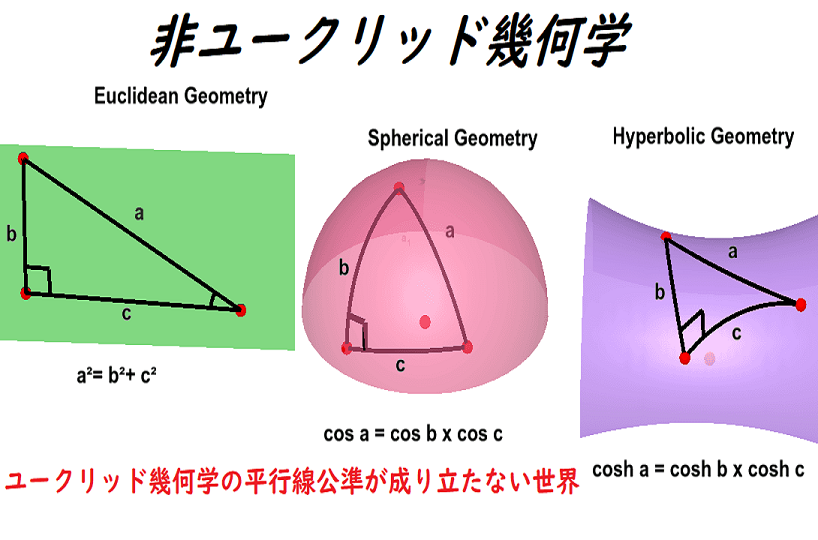
　私の最初の哲学書『幾何学の基礎に関する一考察』(An Essay on the Foundations of Geometry)は、給費研究員資格請求論文に手を入れたもの（推敲したもの）であったが、今の私にとってはいくらか馬鹿げたものに思われる。私はカントの問い「いかにして幾何学は可能か」をとりあげ、空間が周知の三つの変数 －－その一つはユークリッド幾何学の、他の二つは非ユークリッド幾何学の変数であるが,不変の「曲率（measure of curvature）」を保持するという特性を持っている－－ の一つである場合にまたその場合にのみ幾何学は可能である、と結論した。アインシュタイン革命は、こういう考え方に類するものをまったく全て一掃してしまった。アインシュタインの一般相対性理論における幾何学は、私が（それ以前に）不可能だと宣言していたところのものである（あった）。アインシュタインが自説のもととしたテンソルの理論は私にも役に立ったであろうが、アインシュタインがそれを用いるまで私はそれについて聞いたことがなかった。結局、細かい点はともかくとして、この初期の自分の著書の中に何らかの妥当なものがあるとは，私は思わない。
(ウィキペディアの説明：「一般相対論において、アインシュタイン・テンソルは、エネルギーと整合性を持つような方法で、時空の曲率を記述する重力のアインシュタイン方程式の中で発生する。)

Chapter 4: Excursion into Idealism, n.4
My first philosophical book, An Essay on the Foundations of Geometry, which was an elaboration of my Fellowship dissertation, seems to me now somewhat foolish. I took up Kant’s question, ‘how is geometry possible?’ and decided that it was possible if, and only if, space was of one of the three recognized varieties, one of them Euclidean, the other two non-Euclidean but having the property of preserving a constant ‘measure of curvature’. Einstein’s revolution swept away everything at all resembling this point of view. The geometry in Einstein’s General Theory of Relativity is such as I had declared to be impossible. The theory of tensors, upon which Einstein based himself, would have been useful to me, but I never heard of it until he used it. Apart from details, I do not think that there is anything valid in this early book. 　
　Source: My Philosophical Development, chap. 4,1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_04-040.HTM

　優等生試験の後,大学での次の学究上のステップは、給費研究員資格請求学位論文（a Fellowship dissertation）を執筆することであった。私は学位論文の主題として「幾何学の基礎」を選び、非ユークリッド幾何学がカントの超越論的芸術哲学（transcendental aesthetic 超越論的美学）に及ぼす影響について特に注意を払った。この学位論文の執筆作業は（work）は、経済学及びドイツ社会主義に関する執筆作業（work 研究活動）－－ の間に点在させられており（散りばめられており）、それはベルリンに二冬（ふたふゆ）を本拠地を置いて（based upon）、私の最初の著作（公刊したもの）の主題となった。ベルリンでのこの二冬、それから、その翌年（1896年）に妻と一緒のアメリカ旅行は、ケンブリッジ（大学）の偏狭さ（parochialism 地方根性）を治すのに大いに役立ち、また、私がそれ以前に聞いたことのなかったドイツ人の純粋数学に関する著作（及び研究）に気づかせた。それ以前の誓い（注：もう数学の本なんて読まない！という誓い）にもかかわらず、（誓いの後）私は大量の数学書を読んでいた。その多くは、後にわかったことであるが、私の主要な目的には全く無関係なものであった。私はダルブーの『曲面論』（Theory of Surfaces）やディニの『実変数関数論』（Theory of Functions of a Real Variable）や、フランス人の著になる数種の『解析概論』（Cours d’Analyse）や、ガウスの『一般曲面論』（General Theory of Curved Surfaces）やグラスマンの『線形延長論延長論』（Ausdehnungslehre）を読んだ。このグラスマンの本は,ホワイトヘッドによって導かれたものである。ホワイトヘッドの『普遍的代数論』(Universal Algebra)は私を大いに興奮させたが、その本はその後（ラッセル夫妻訪米時以後）すぐに出版されており（注：『普遍的代数論』は1898年に出版）、グラスマンの体系に大いに関連していた。けれども,私は、応用数学の方が純粋数学よりも価値のある研究であると（当時）信じていた。なぜなら，応用数学の方が －－私はヴィクトリア王朝時代の楽観主義でそう考えていたのだが－－ 人間の幸福をより増進しそうだからであった。私はクラーク・マックスウェル(著)『電気と磁気』を注意深く読み、ヘルツの『力学原理』を研究し、ヘルツが電磁波を作り出すことに成功したときは大いに喜んだ。J. J. トムソンの実験的研究は、大いに私の興味をひいた。私はまた、自分の目的により関連することが（後で）わかった著作、たとえば、デデキントやカントールやフレーゲの著作 －－（学位論文執筆において）私のより助けになった可能性があったが－－ は後になって（学位論文執筆後に）知ったのである。

Chapter 4: Excursion into Idealism, n.3
After the Tripos, the next academic step was the writing of a Fellowship dissertation. I chose for my subject ‘The Foundations of Geometry’ , and paid special attention to the effect of non-Euclidean geometry on Kant’s transcendental aesthetic. My work on this dissertation was interspersed with work on economics and on German social democracy, which was the subject of my first book, based upon two winters in Berlin. These two winters, and a journey to America with my wife in the following year (1896), did much to cure me of Cambridge parochialism, and made me aware of German work in pure mathematics which I had not previously heard of. In spite of my earlier vow, I read a very great deal of mathematics – much of it, as I afterwards discovered, quite irrelevant to my main purpose. I read Darboux’s Theory of Surfaces, Dini’s Theory of Functions of a Real Variable, and several French Cours d’Analyse, Gauss’s General Theory of Curved Surfaces, and Grassman’s Ausdehnungslehre, to which I was led by Whitehead, whose Universal Algebra, which greatly excited me, was published shortly after this time and was largely concerned with Grassman’s system. I was, however, persuaded that applied mathematics is a worthier study than pure mathematics, because applied mathematics – so, in my Victorian optimism, I supposed – was more likely to further human welfare. I read Clerk Maxwell’s Electricity and Magnetism carefully, I studied Hertz’s Principles of Mechanics, and I was delighted when Hertz succeeded in manufacturing electro-magnetic waves. J. J. Thompson’s experimental work interested me greatly. I read, also, works that proved more relevant to my purpose, such as those of Dedekind and Cantor, Frege, who might have helped me more, I did not know of until later.
　Source: My Philosophical Development, chap. 4,1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_04-030.HTM

　私が学部生であった時，ケンブリッジ（大学のトリニティ・コレッジ）における数学教育は間違いなく悪いものであった。その劣悪さは、一部は優等生試験における成績順位制（order of merit 優劣の順位）のせいであったが，その後しばらくして廃止された。多種多様の受験生の能力の間に精密に区別（nice descrimination）をつける必要性が「書物による研究（学習）」よりも「問題を解くこと」の強調へと導いた（のである）（訳注：テストをして点数をつければ差がはっきりするため）。数学の定理(theorem)に対して当時与えられていた「証明（法）」(proofs)は、論理的な知性に対する侮辱であった。実際、数学の全内容（全ての主題）が、優等生試験で点をかせぐための（pile up marks）、上手な技（clever tricks）のよせ集めとして提示されていた。これら全てが私に与えた影響によって、私は数学を嫌なものだと考えさせた。私は優等生試験を終ると、自分が持っていた数学の本を全て売り払い、もう二度と数学の本は見ないぞと誓をたてた。そうして，ケンブリッジの４年目に、心からの喜びをもって、私は哲学の素晴らしい世界へと飛び込んだ（のであった）。 　（当時）私に向けられた（加えられた）影響は，唯一の例外を除いて，全て(brought to bear upon me)、カントあるいはヘーゲルの,ドイツ観念論の方向（方面）であった(in the direction of)。ただし、ただびとつの例外があり、それは、功利主義者（ベンサム主義者）の最後の生残りのヘンリー・シジウィック（Henry Sidgwic, 1838-1900）であった。私は、当時。他の若い人々と同様に（in common with ～と共通して）、シジクイックに対して、当然払うべき敬意を十分払わなかった。我々は彼を「老シジ(シジ爺)」と呼び、ただの時代遅れの人間とみなしていた。私を教育するにあたって最も関係していた人は、ジェームズ・ウォードと G. F. スタウトであり，前者はカント主義者であり、後者はヘーゲル主義者であった。ブラッドリ(F. H. Bradley, 1846-1924)『現象と実在』が当時出版されたが、スタウトは、この本は存在論（ontology）に関して人間が可能な限りのことを成し遂げたものであると言った。けれども、これら二人のいずれも、マクタガート（が私に与えた影響）ほどには私に影響を与えなかった。マクタガート(John M. E. McTaggart, 1866-1925)は、それ以前に私を満足させていたかなり粗雑な経験論に対する、ヘーゲル主義の側からの反論（回答）を持ち合わせていた。彼は論理によって世界が善であり魂が不死であることを、証明できる、と言った。しかし、彼も認めたが，その証明は長くて難解なものであった。相当長く哲学をした後でなければ、その証明を理解することは望みえないものであった。私は彼の影響力に反発したが、徐々に抵抗を弱め（減じ）、1894年（注：ラッセル22歳）の人文学優等生試験の直前には、半ばカント的、半ばヘーゲル的な形而上学の立場に完全に移っていた.

Chapter 4: Excursion into Idealism, n.2
The mathematical teaching at Cambridge when I was an undergraduate was definitely bad. Its badness was partly due to the order of merit in the Tripos, which was abolished not long afterwards. The necessity for nice discrimination between the abilities of different examinees led to an emphasis on ‘problems’ as opposed to ‘bookwork’. The ‘proofs’ that were offered of mathematical theorems were an insult to the logical intelligence. Indeed, the whole subject of mathematics was presented as a set of clever tricks by which to pile up marks in the Tripos. The effect of all this upon me was to make me think mathematics disgusting. When I had finished my Tripos, I sold all my mathematical books and made a vow that I would never look at a mathematical book again. And so, in my fourth year, I plunged with whole-hearted delight into the fantastic world of philosophy. All the influences that were brought to bear upon me were in the direction of German idealism, either Kantian or Hegelian, with one single exception. The exception was Henry Sidgwick, the last survivor of the Benthamites. At the time, I, in common with other young people, did not give him nearly as much respect as he deserved. We called him ‘Old Sidg’ and regarded him merely as out of date. The two men who had most to do with teaching me were James Ward and G. F. Stout, the former a Kantian, the latter a Hegelian. Bradley’s Appearance and Reality was published at this time, and Stout said that this book accomplished as much as is humanly possible in ontology. Neither of these two men, however, influenced me as much as McTaggart did. McTaggart had Hegelian answers to the rather crude empiricism which had previously satisfied me. He said he could prove by logic that the world is good and the soul immortal. The proof, he admitted, was long and difficult. One could not hope to understand it until one had studied philosophy for some time. I stood out against his influence with gradually diminishing resistance until just before my Moral Sciences Tripos in 1894, when I went over completely to a semi-Kantian, semi-Hegelian metaphysic. 　
　Source: My Philosophical Development, chap. 4,1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_04-020.HTM

　J. S. ミル以外の職業哲学者（注：professional philosophers 哲学の著作や講義などで生計をたてている専門の哲学者／別の職業をもって哲学をやっている者は市井の哲学者）とその著書において出会ったのは,ま,た直接会ったのは（in person）、1890年10月（注：ラッセル18歳）にケンブリッジ（大学）に行ってから（入学してから）が初めてのことであった(注：not until ～になっって初めて／写真は1891年、１９歳のラッセル)。（大学入学後の）最初の３年間は自分の時間の大部分を数学にあてなければならなかったけれども、かなりの量の哲学書の読書と大量の哲学上の議論をなんとかやり抜くことができた（managed to get through）。（オックスフォード大学の学寮の一つである）マートン学寮の哲学教員（don）でブラッドリの弟子であったハロルド・ヨアキム（Harold Joachim）はハスルミア（注：Haslemere：英国サリー州ウェイバリー地区の町）における我々の隣人で、私の叔父の義兄弟となった。私は哲学に興味をもっていることを彼に話した。すると彼は、大変親切にも、読むべき書物のリストを私にくれた。そのリストのなかで二つの項目（items）だけを今でも記憶している。一つブラッドリの『論理学』であり、彼は良書であるが難解だと言った。もう一つはボサンケー（Bernard Bosanquet）の『論理学』であり、もっと良いがもっと難解だ、と彼は言った。おそらくかれは驚いたことだろうが、彼がくれたリストの本を，私はどんどん読み進めた。しかし、私のこの哲学書の読書は偶然の出来事によってしばらくの間中断された。1892年の始めに、私は軽いインフルエンザ（流行性感冒）にかかったが、これはその後数ヶ月間（３，４ヶ月間）全く気力をなくさせるととも，何事に対してもまったく興味なくさせた。その時の私の研究（work 学業の結果＝成績）は悪かった。そうして，私はインフルエンザにかかったこと及びその余波について誰にも話さなかったので、哲学書の読書が私の数学を損なったのだろうと（周囲の）人々は考えた。前に何を読むぺきかについて相談したことのあったジェイムズ・ウォードは,私を呼んで（注：James Ward sent for me 私に自分のところに来るように指示し）「優等生は優等生である(a Wrangler is a Wrangler. )」と言った。同一律(注：A=A)のこの一例（実例）から、彼は私が数学の優等生試験を済ますまで哲学書をもう読まないほうがよいという推論を引きだした。その結果ウォードが注意を与えてくれた時に心配されていたほど悪い成績を私は取らなかった。
Chapter 4: Excursion into Idealism, n.1
It was not until I went up to Cambridge, in October 1890, that I came across professional philosophers other than Mill, whether in their books or in person. Although during my first three years I had to give the bulk of my time to mathematics, I managed to get through a fair amount of philosophical reading and a large amount of philosophical arguing. Harold Joachim, a philosophy don at Merton and a disciple of Bradley, was our neighbour at Haslemere and became my uncle’s brother-in-law. I told him of my interest in philosophy, and he very kindly gave me a list of books to read. I remember only two items in the list: one was Bradley’s Logic which, he said, was good but hard; the other was Bosanquet’s Logic which, he said, was better but harder. Probably to his surprise, I proceeded to read the books on his list. But my reading of philosophy was interrupted for a time by an accidental occurrence. At the beginning of 1892 I had a slight attack of influenza which left me for several months completely without energy or interest in anything whatever. My work at this time was bad, and, as I had not told anybody about the influenza and its aftermath, it was supposed that reading philosophy was what had spoilt my mathematics. James Ward, whom I had consulted as to what I should read, sent for me and told me that a Wrangler is a Wrangler. From this instance of the law of identity he drew the inference that I had better read no more philosophy till after my mathematical Tripos, with the result that I did not do so badly in it as had been feared when he gave his advice.
　Source: My Philosophical Development, chap. 4,1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_04-010.HTM

　私が疑いを持ったのは、神学に関してだけではなく，数学に関してもだった。ユークリッド(幾何学)の証明のいくつか、特に重ねあわせの方法を用いる証明は、私にはとてもあやふやであるように見えた（あやしく思われた）。私の家庭教師(注：tutor)の一人は、非ユークリッド幾何学について話してくれた。私は非ユークリッド幾何学については,それから何年も後まで,それが存在しているという単なる事実以外,何も知らなかったけれども、そういう学科（subject 主題分野）があるということを知って非常に興奮し，知的な喜び見出したが，同時に，それは幾何学上の疑問について,私の不安をかきたてる（disquieting ）源泉であった。私に微積分(Infinitesimal calculus　微積分学)を私に教えた人たち（教師たち）はその基本定理の正しい証明法を知っておらず、当時公認されていた詭弁の数々（sophistries）をひとつの信仰個条として受けいれるように,私を説得しようと努めた。私はこの微積分（学）が実際に機能する（うまくいく）ことはわかったが、なぜそれがうまくいくのか理解することがまったくできなかった。けれども，私は技術的なスキルの獲得に大きな喜びを見出し，大部分の時間（期間）、私は自分の疑いを忘れていた。そしてその疑いは,ある程度,私を大変喜ばした一冊の書物、即ち、W, K. クリフォードの『精密科学の常識』（Common Sense of the Exact Sciences）によって安らかにさせられた（laid to rest 埋葬された；休ませられた）。 　この数年間,青年期の（青年期にありがちな）みじめな気持に満たされたけれども、私は，この数年間，知識（の獲得）及び知的業績（達成）への欲求によって前進し続けた（kept going)。私は、混乱を除去でき、それができれば機械が仕事をし，正義が分配を統制する世界となり（注：経済的平等が実現し）、全ての人々が幸福になれると、考えた（のである）。私は、早晩，完全な数学（疑うところが全く存在しない数学）に到達し、そうして,確実性の範囲を数学から他の科学へ徐々に拡張してゆくことができる、と期待した。そしてこの３年間(18歳でケンブリッジにあがるまでの)に徐々に神学に対する興味は減ってゆき、神学上の通説の最後の痕跡を投げすてた時には，本当に救われたように感じた（安堵感を覚えた）のであった。
Chapter 3: First Efforts, n.13
It was not only as to theology that I had doubts, but also as to mathematics. Some of Euclid’s proofs, especially those that used the method of superposition, appeared to me very shaky. One of my tutors spoke to me of non-Euclidean geometry. Although I knew nothing of it, except the bare fact of its existence, until many years later, I found the knowledge that there was such a subject very exciting, intellectually delightful, but a source of disquieting geometrical doubt. Those who taught me the infinitesimal Calculus did not know the valid proofs of its fundamental theorems and tried to persuade me to accept the official sophistries as an act of faith. I realized that the calculus works in practice, but I was at a loss to understand why it should do so. However, I found so much pleasure in the acquisition of technical skill that at most times I forgot my doubts. And, to some extent, they were laid to rest by a book which greatly delighted me: W. K. Clifford’s Common Sense of the Exact Sciences. Although filled with adolescent misery, I was kept going in these years by the desire for knowledge and for intellectual achievement. I thought that it should be possible to clear away muddles, and that then everybody would be happy in a world where machines would do the work and justice would regulate distribution. I hoped sooner or later to arrive at a perfected mathematics which should leave no room for doubts, and bit by bit to extend the sphere of certainty from mathematics to other sciences. Gradually during these three years my interest in theology grew less, and it was with a genuine sense of relief that I discarded the last vestiges of theological orthodoxy.
　Source: My Philosophical Development, chap. 3,1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_03-130.HTM

　この時代（注：ラッセルが15歳から17歳の時）における私の精神は、３つの異なる世紀（注：17,18,19世紀）に属する物の見方と感じ方とを一つに結合しようとする試みから生じる混乱状態（の中）にあった。上述の（日記帳からの）抜き書きが示すように、私の考え（思考）は、荒っぽい形態であるが、デカルトの考え（思考）に非常に似通った方向をとっていた。私はデカルトの名前には親しんでいたが、しかし、私は彼をデカルト座標の発明者としてだけ知っており、彼が哲学書を書いていたとは（当時）気づいていなかった。自由意志（を認めること）は神の全能（性）を侵害するという理由によって自由意志を私が拒否することは、スピノザの哲学に似た哲学に私を導いたかも知れなかった。私はこのような17世紀的な見方（見解）へ,そういう見方を17世紀において生み出したと同じ理由（根拠）によって、導かれた。即ち、力学の法則に親しんだこと，また,力学の法則が物質のあらゆる運動を説明するという信念に親しんだこと（によるものである）。けれども，しばらくして、私は神の存在を信じなくなり、さらに18世紀フランスの「哲学者たち」（French Philosophes）の主張により近いものへと進んだ。私は合理主義の情熱的な信奉者であるという点で彼らと同意した（一致した）。私はラプラス(Pierre-Simon Laplace, 1749-1827)の「計算者」（Laplace’s calculator ）を好んだ。私は迷信と考えられるものを嫌った。そうして，私は，（人間の）理性と機械とを組み合わせることにより人間が限りなく完全になりうる、という考えを深く信じた。これらは全て、熱烈なものであったが、本質的に感情的なものではなかった。けれども、私は、これらの考えと並んで、知的な支持を自らまったく見出すことができないものに対して,とても生き生きとした感情的態度を抱いていた。私は宗教的信条を失ったことを残念に思った。私は野性的な情熱をもって自然の美を愛した。私は，ワーズワースやカーライルやテニスンの,宗教に対する感傷的な弁護（apologies 弁明）を － 知的には非常に明確に拒否しながらも－ （当時は）共感をもって読んだ。バックルを別にすると、J. S. ミルの『論理学』を読むまでは、知的誠実性をそなえていると思われる書物には出あったことがなかった。しかし、それにもかかわらず、私は自分が受けいれることができない修辞（レトリック）によって動かされていたのであり，カーライルの「永遠の否定(No)」と「永遠の肯定(Yea)」は －心の底ではそれらはナンセンスだと考えていたにもかかわらず－ 私には大変すばらしいものに思われた。。当時私の知っていた著作家の中では、P. B. シェリーだけが、全面的に私の気性にあっていた。シェリーはその長所において私に一致していただけでなく,その欠点においても一致していた。彼の自らを憐れむ気持ち、彼の無神論は、いずれも私を慰めた。（結局）私は、17世紀の(合理主義的な)知識と、18世紀の信条と、19世紀の（浪漫はの）熱情とを、一つの調和ある全体にまとめあげることがまったくできなかった（のである）。
Chapter 3: First Efforts, n.12
My mind at this time was in a state of confusion derived from an attempt to combine points of view and ways of feeling belonging to three different centuries. As the above extracts show, my thinking was, in a crude form, along lines very similar to that of Descartes. I was familiar with the name of Descartes, but I knew him only as the inventor of Cartesian co-ordinates, and was not aware that he had written philosophy. My rejection of free will on the ground that it infringed God’s omnipotence might have led me on to a philosophy like that of Spinoza. I was led to this seventeenth-century point of view by the same causes which had originally produced it: namely, familiarity with the laws of dynamics and belief that they accounted for all the movements of matter. After a time, however, I came to disbelieve in God, and advanced to a position much more like that of the eighteenth-century French Philosophes. I agreed with them in being a passionate believer in rationalism; I liked Laplace’s calculator; I hated what I considered superstition; and I believed profoundly in the perfectibility of man by a combination of reason and machinery. All this was enthusiastic, but not essentially sentimental. I had, however, alongside of this, a very vivid emotional attitude for which I could find no intellectual support. I regretted my loss of religious belief; I loved natural beauty with a wild passion ; and I read with sympathetic feeling, though with very definite intellectual rejection, the sentimental apologies for religion of Wordsworth, Carlyle and Tennyson. I did not come across any books, except Buckle, until I read Mill’s Logic which seemed to me to possess intellectual integrity. But, nonetheless, I was moved by rhetoric which I could not accept. Carlyle’s ‘Everlasting No’ and ‘Everlasting Yea’ seemed to me very splendid, in spite of my thinking that at bottom they were nonsense. Only Shelley, among the writers whom I knew at that time, was wholly congenial to me. He was congenial to me not only in his merits, but also in his faults. His self-pity and his atheism, alike, consoled me. I was quite unable to combine into a harmonious total seventeenth-century knowledge, eighteenth-century beliefs and nineteenth-century enthusiasms. 　
　Source: My Philosophical Development, chap. 3,1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_03-120.HTM