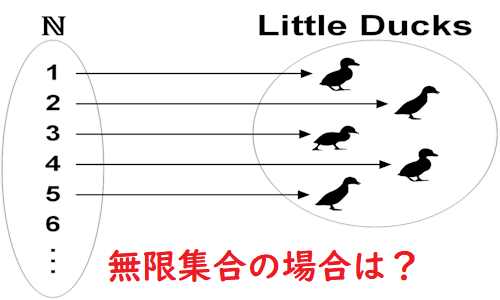
上記の数の定義(法)は、きわめて重要な、さらなるもうひとつの利点を提供する。その利点というのは、無限数に関する多くの困難(問題)に終止符を打つということ(利点)である。項(terms)を一つずつ取りあげて数えることから数が得られると考えられていた間は(While numbers were derived from counting …)、一度に一つずつとって(one at a time)枚挙しつくことのできないような集合の(要素である)数を思い描くことは困難であった。たとえば,我々は、数えることによって、有限数(finite numbers)の終り(最後の数)に到達することは不可能である。どれほど数え続けても、常にそれより大きな数が存在している。それゆえ、数は数えることから生ずると考えられていた間は、有限数が(最大)いくつあるかについて語ることは不可能であると思われた。けれども、今や、数えることはある一つの集合の中にどれだけ多くの項があるかを見出すための単なる一つの方法にすぎず、それはたまたま(数が)有限であるような集合にのみ適用しうるものであるこように思われる。数えることのロジック(論理)を、新しい学説に適合するように考え直すと、次のようになる。たとえば、いまポンド紙幣(pound notes)を数えているとしてみよう。意志行為によって(act of will 無意識にではなく意志をもって)、我々は数枚の紙幣と、数 l、2、3等々との間に、一対一の関係をつけ、もう残った紙幣がないところまで対応付けを行う。そうすると(then)上記の我々の定義(法)に従い(in accordance with)、紙幣の数は、あなたが言及してきた数の数(number of numbers)と同一であることがわかる(注:1,2,3,4,5と5まで数えてもう紙幣が残っていなければ「5」がその数になるということ)。そして、もし我々は1から数え始めて、どの数をもスキップしないで進んだのであれば、言及した数の数は、最後に挙げた数である(注:数え方はいろいろあるためにこのように言っている)。このやり方を、無限集合に適用することはできない。なぜなら、我々の生命はそれほど長くないからである。しかし数えるということはもはや絶対に必須ではないので、そのことはまったく気にする必要はない。(that need cause you no concern)
Chapter 6: Logical Technique in Mathematics, n.8
The above definition of numbers offers a further advantage which is of profound importance, and that is that it puts an end to difficulties concerning infinite numbers. While numbers were derived from counting, which takes terms one by one, it was difficult to conceive of the numbers of collections which could not be exhaustively enumerated one at a time. You cannot, for example, come to an end of the finite numbers by counting: however long you go on, there are always larger numbers to come. Therefore, so long as numbers were derived from counting, it seemed impossible to speak of the number of finite numbers. Now, however, it appears that counting is only one way of discovering how many terms there are in a collection, and is only applicable to such collections as happen to be finite. The logic of counting, as fitted into the new theory, is as follows: suppose, for example, that you are counting pound notes. By an act of will, you establish a one-one relation between the several notes and the numbers 1, 2, 3, etc., until there are no notes left. You then know, in accordance with our definition, that the number of notes is the same as the number of numbers that you have mentioned, and, if you have begun with 1 and gone on without skipping, the number of numbers that you have mentioned is the last number that you have mentioned. You cannot apply this process to infinite collections because life is not long enough. But, as counting is no longer essential, that need cause you no concern.
Source: My Philosophical Development, chap. 6:1959.
More info.:https://russell-j.com/beginner/BR_MPD_06-080.HTM