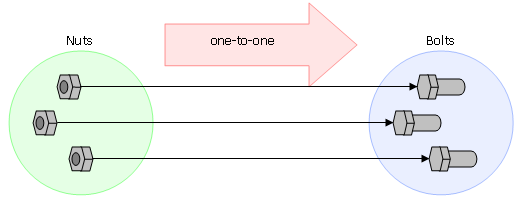
数についての（ペアノ）以前の理論は、0と1とについて、常に困難に陥った（陥っていた）。そして、まず私が感心したのは、これらの困難を扱うペアノの手腕であった。しかし、この新しい観点の全帰結を私が引き出したのはそれからかなり経ってからのことであった。数学において（は）「集合」（classs）について考えることは便利であり（であるので）、長い間私は集合と命題関数とを区別する必要があると考えていた。けれども、最終的にはこの区別が技術的工夫として以外には不必要であるとの結論に達した。「命題関数」という句は、多分、不必要に恐ろしげに（formidable）聞こえるかも知れない。多くの場合、それは「特性（属性）」（property）という語で言いかえることが可能である。その結果として（thus それゆえ）我々は、各々の数は諸特性のなかの一特性（a property of certain properties）であると言ってよいであろうが、しかし、最終的な分析における場合以外は、「集合」(class)という語を使い続けることが、いっそう容易であろう。 　上記の考察によって私が導かれた数の定義は、それよりも16年も早く（前に）、フレーゲによって定式化されていた（はっきりと述べられていたが、私はそのことを、私がそれを再発見したおよそ一年後まで知らなかった。私は（数の）２を「あらゆる対（couple つい）の集合」と定義し、(数の）３を「あらゆる三つ組（trio）の集合」等々、と定義した。「対」というのは、xとyという要素をもつ集合であって、xとyとは同一でなく、かつもし第三者zがその集合の要素であるなら、zはxかyのいずれかと同一であるような集合である。一般に一つの数とは、「類似性（相似性）」（similarity）と言われる特性（属性）をもつところの,集合の集合(a set of classes)である。「類似性（相似性）」は次のように定義される。即ち、二つの集合はそれらの諸項（terms）を一つずつ対(つい)にする方法がある（存在する）とき、類似的（相似）であると言われる。たとえば、一夫一婦制の国においては(in a monogamous country)、結婚している男の数は結婚している女の数と同数であるということを、男女がそれぞれ何人いるかを知らずとも、知ることが可能である（注：現代では結婚が男女の組み合わせ以外もあるようになったため、このように断言できなくなっている）。（私は夫を失った妻や妻を失った夫を勘定に入れていない。）　さらにまた、一人の人が片足を失っていないなら、彼のもっている右足の靴の数は、左足の靴の数と同じであることはかなりの場合確かであろう。また、ある会の出席者が皆椅子に坐っており、かつ空いた椅子が一つもなければ、椅子の数は椅子に坐っている人間の数と同じに違いない。これらすべての場合において、一方の集合の要素と他方の集合の要素との間に、いわゆる一対一の関係が存在するのであり、そういう一対一の関係の存在こそ「類似性」といわれるものである。そこで任意の集合の数とは、その集合に類似な集合の全てであると定義される。

Chapter 6: Logical Technique in Mathematics, n.6 The older theories of number always got into difficulties over 0 and 1, and it was Peano’s capacity of dealing with these difficulties that first impressed me. But it was a good many years before I drew the full consequences of the new point of view. It is convenient in mathematics to think of ‘classes’, and for a long time I thought it necessary to distinguish between classes and propositional functions. Ultimately, however, I came to the conclusion that this distinction is unnecessary except as a technical device. The phrase ‘propositional function’ sounds perhaps unnecessarily formidable. For many purposes one can substitute the word ‘property’. Thus, we may say that each number is a property of certain properties, but, except in ultimate analysis, it is perhaps easier to continue to use the word ‘class’. The definition of numbers to which I was led by the above considerations had been formulated by Frege sixteen years earlier, but I did not know this until a year or so after I had re-discovered it. I defined 2 as the class of all couples, 3 as the class of all trios, etc. A couple is defined as a class of which there are members x and y, x is not identical with y, and, if z is a member of the class, then z is identical with x or with y, A number, in general, is a set of classes having the property which is called ‘similarity’. This is defined as follows; Two classes are similar if there is a way of coupling their terms one to one. For example, in a monogamous country, you can know that the number of married men is the same as the number of married women, without having to know how many there are of either (I am excluding widows and widowers). Again, if a man has not lost a leg, you may be pretty sure that the number of his right-hand shoes is the same as the number of his left-hand shoes. If every member of a company has a chair to sit on and there are no empty chairs, the number of chairs must be the same as the number of people sitting on them. In all these cases there is what is called a one-one relation between the terms of one class and the terms of another, and it is the existence of such a one-one relation which is defined as similarity. The number of any class is defined as all the classes that are similar to it. 　
　Source: My Philosophical Development, chap. 6：1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_06-060.HTM

　算術の哲学は、フレーゲ以前のすべての著者によって間違って考えられていた。彼らの全てが犯した誤まりはとても自然なものであった。彼らは数を数えることによって生ずるものであると考えた。しかし、一（ひとつ）として数えられるものは、同様に多（数）としても同様に（equally well 負けず劣らず）数えられるゆえに、絶望的な困難に陥った。たとえば、イングランドにどれだけのフットボール・クラブ（注：英国ではサッカー・クラブのこと）があるか？という問いをとりあげてみよう。この間いに答える際、我々は各クラブを１つ（１チーム）としてとり扱う。しかしある一つのフットボール・クラブがどれだけの会員をもつかと問うことも同様に質問してもよいであろう（may just as well）。その場合には、我々はそのクラブを（部分を持たない一つのものではなく）多として扱っている。また（さらに）Ａ氏がこれらのクラブの中の一つに属する会員である場合、彼はそれ以前には１（人）として数えられているが、今度は、そのＡ氏がどれだけの数の分子から成っているか、と同様に正当に問うことが可能であろう（問うてもいいだろう）。そうして、その場合には、Ａ氏は多として数えられる（ことになる）。こういうわけで、数える際に何ものかを１たらしめるものは、そのものの物理的性質ではなく、「これは何の一例であるか？(Of what is this an instance?)」という問いなのである（注：人間の例としてなら一人、分子の例としてなら多数、となる）。数えることによって、我々が到達する数は、何らかの集合の数であり、その集合は我々がそれを（その要素/成員）数える前にどのような数であれ数を持っているのである（注：数えなくても人間なら一人、目の数なら２個、背骨の数は◯◯個、・・・等々）。集合が多であるのは、ただ何らかのものの多数の例としてである。そしてその集合自身（それ全体を一つとして考えた場合）はまた何か他の（別の）ものの例でありうるのであり、その例としては 一（つ）として数えられる（in enumeration 列挙すると、数えると）。このようにして，我々は「集合とは何か？」，また，「例とは何か？」という問いに対峙することを強いられる。この二つの問いはいずれも、命題関数（函数）という方法（手段）を用いないでは理解することができない。命題関数（函数）というのは、一つの変項を含む式(an expression 数式や論理式)であり、その変項に一つの値が指定される（割り当てられる）やいなや、一つの命題となるものである。たとえば、「xは人間である」は、一つの命題函数である。そして x の代りにソクラテスやプラトンやその他の誰かを置くと、我々は命題を得るのである。我々はまた，xを、人でないところのもので置きかえることもでき、そしてそれでもやはり（still）一つの命題を得るが、その場合には偽なる命題を得るわけである（注：たとえば、自宅の犬のポチを代入すると、「愛犬のポチは人間である」という偽命題ができる）。命題関数（函数）とは、一つの式（注：an expression 数式や論理式／因みに、みすず書房刊の野田訳では「表現」と訳出されている。）にすぎない。それは、それだけでは何ものをも表さない。しかし，それは、真偽いずれにせよ，何ものかを主張する文の一部を形作ることが可能である。「xは使徒であった」は、何ごとも意味しないが、「xは使徒であった』を真ならしめるような値が12ある（注：１２使徒のこと）」というのは完全（完璧）な文である。同様な考察（similar consideration）が、例（実例）という概念にも当てはまる。我々が何ものかを一つの例と見るとき、我々はそれをある命題関数の変項のもちうる一つの値と考えている。たとえば「ソクラテスは人間の一例である」と私が言うとき、私はソクラテスが、「x は人間である」を真にするxの一つの値である、ということを意味している。(中世の)スコラ哲学者は「一」（One）と「存在」（being）とは交換可能な名辞(terms)であるという趣旨の（to the effect that）格率（a maxim）を立てていた。この格率は、それが信ぜられているかぎり、(数の）１を定義することを不可能にした。実を言えば、「存在」は無用な（役に立たない）語であり、この無用な語が間違った仕方であるものに適用されると、それは一であるとともに多である，ということになりがちである。一は一つの特性（特質）であるが、それはもの（物）の特性（特質）ではなく、ある種の命題関数（函数）、つまり、次のような特性（特質）をもつ命題関数（函数）の特性（特質）である。（即ち）その関数を真にするxがあり、しかも、もしyがその関数を真にするならば、y は x と同一である、という特性（特質）である。これがただ一つの値をもつ関数（unitary function）の定義であり、数１はある種の関数がもつところの「ただ一つの値をもつ」（being unitary）という特性（特質）なのである。同様にして「空（くう）なる関数」（null-function）とは、xのあらゆる値に対して偽となる関数であり、0 とは「空なる関数である」という特性（特質）なのである。

Chapter 6: Logical Technique in Mathematics, n.5 The philosophy of arithmetic was wrongly conceived by every writer before Frege. The mistake that all of them made was a very natural one. They thought of numbers as resulting from counting, and got into hopeless puzzles because things that are counted as one can equally well be counted as many. Take, say, the question, ‘How many football clubs are there in England？’ In answering this question, you treat each club as one, but you may just as well ask: ‘How many members has such and such a football club.’ In that case, you treat the club as many. And, if Mr A is a member of one of these clubs, although he counted as one before, you may ask just as legitimately, ‘How many molecules make up Mr A?’ And, then, Mr A counts as many. It is obvious, therefore, that what makes anything one from the point of view of counting is not its physical constitution but the question, ‘Of what is this an instance?’ The number that you arrive at by counting is the number of some collection, and the collection has whatever number it does have before you count it. It is only qua many instances of something that the collection is many. The collection itself will be an instance of something else, and qua instance counts as one in enumeration. We are thus forced to face the question, ‘What is a collection?’ and ‘What is an instance?’ Neither of these is intelligible except by means of propositional functions. A propositional function is an expression containing a variable and becoming a proposition as soon as a value is assigned to the variable. For example, ‘x is a man’ is a propositional function. If, in place of x, we put Socrates or Plato or anybody else, we get a proposition. We can also replace x by something that is not a man and we still get a proposition, though in this case a false one. A propositional function is nothing but an expression. It does not, by itself, represent anything. But it can form part of a sentence which does say something, true or false: ‘x was an Apostle’ says nothing, but ‘there are twelve values of x for which “x was an Apostle” is true’ is a complete sentence. Similar considerations apply to the concept instance. When we consider something as an instance, we are considering it as a possible value of a variable in a propositional function. If I say, ‘Socrates is an instance of Man’ I mean Socrates is a value of x for which ‘x is a man’ is true. The Scholastics had a maxim to the effect that one and being are convertible terms. This maxim, so long as it was believed, made it impossible to define 1. The truth is that being is a useless word, and that the kind of things to which this useless word is applied by those who mistakenly use it are just as apt to be many as to be one. One is a characteristic, not of things, but of certain propositional functions, namely, of those propositional functions which have the following property: there is an x which makes the function true and which is such that, if y makes the function true, y is identical with x. This is the definition of unitary functions, and the number 1 is the property of being unitary which certain functions possess. Similarly, a null-function is one which is false for all values of x, and 0 is the property of being a null-function.
　Source: My Philosophical Development, chap. 6：1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_06-050.HTM

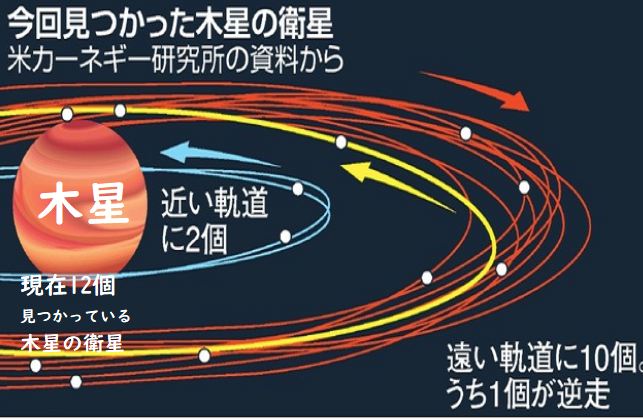
　私がベアノから学んだ第二の重要な進歩は、一つの要素（member 成員）から成る集合（class）はその一つの要素（成員）と同一のものではない、ということであった。たとえば、「地球の衛星」は一つの集合であり、ただ一つの要素（成員）、即ち月を持つのみである(注：因みに木星は12個の衛星を持っているので、集合と一つの要素である一つの衛星とは等価でないことがわかりやすい)。しかし一つの集合をそれの唯一の要素と同一視することは、集合の論理学に、従って、数の論理学に　－－というのは数が適用されるのは集合だからである－－ 全く解決不可能な問題を導き入れる。「地球の衛星」と「月」とを同一視することが不適切であることは、一度指摘されれば容易に理解される。「地球の衛星」という句は、たとえ第二の衛星が発見されても（if = even if）、その意味を変ずることはないであろう。それはまた、天文学を理解するが地球が衛星を持つことを知らない（知らなかった）ような人にとっても、無意味ではないであろう（注：destitute of meaning 意味を欠くようなことはないであろう）。これに反して、月についての陳述は、－「月」（The Moon）という語を固有名(a name)ととってよいのなら、月を承知している者以外の人々にとっては、無意味である（注：「衛星」と言えばわかるが、◯×△（例：ヘベレケポンポン）と知らない言葉を言われても何を言っているかわからない）。そういう人々にとっては、「月（The Moon）」という語は、それが「地球の唯一の衛星」という句と同等である（相当する）という説明が与えられなければ、無意味な雑音であろう。そうして（しかも）,たとえ「月」という語の代りに「地球の唯一の衛星」という句が代用されるとしても（置き換えられたとしても）、月についての陳述は、「今夜は月が明るい」と我々が言う時に、その月についての陳述が私やあなたに対して持つような意味を、持たないであろう（注：if = even if／つまり、月」という固有名と、「地球の唯一の衛星」という記述＝説明とは同じではない、とラッセルは言っている。／因みに、みすず書房版の訳では、野田氏は、「if = even if」としてとらずに、「もし～ならば～だろう」と訳されているのでピンとこない訳となっている）。「月」の代りに月についての「記述」を代用する人（置き換える人）は、概念と繋がっている領域にいるのであって、「月が明るい」という人のように、感覚の世界との直接な接触をしていない（注：前者は記述によって得ている知識であり、後者は直接知に該当する／ラッセルの哲学において重要な、記述知と直接知の区別の重要性／他の例で言うと、記述的に「現在の日本の総理」という場合と、安倍総理を目の前にして「安倍晋三」という場合の違いに相当）。この点において、我々が今関心を持っている（関わっている）区別は、「ソクラテスは死ぬものである」と「全てのギリシャ人は死ぬものである」という，先に述べた区別と、一定の類似性を持っている。本書の読者は、上記の（このような）区別は学者のもったいぶった言い方（衒学）にすぎないと考えたくなるかも知れない（may be disposed to think）。私は今やこの区別はそういった学者の衒学的な言い回しではない理由を説明することに努めなければならない。

Chapter 6: Logical Technique in Mathematics, n.4
The second important advance that I learnt from Peano was that a class consisting of one member is not identical with that one member. ‘Satellite of the Earth’, for instance, is a class and it has only one member, namely, the Moon. But to identify a class with its only member is to introduce utterly insoluble problems into the logic of collections and, therefore, of numbers, since it is to collections that numbers apply. The impropriety of identifying ‘Satellite of the Earth’ with the Moon is easily seen when it has once been pointed out. The phrase, ‘Satellite of the Earth’, would not alter its meaning if a second satellite were discovered; nor would it be destitute of meaning for a person who understood astronomy but did not know that the Earth had a satellite. Statements about the Moon, on the other hand, if we may take ‘The Moon’ as a name, are meaningless except to those who are aware of the Moon. To others, ‘The Moon’ would be a meaningless noise unless it were explained to be equivalent to the phrase ‘The only satellite of the Earth’; and if this explanation were substituted, statements about the Moon would not have the meaning that they have for you and me when we say, ‘The Moon is bright tonight’. The man who substitutes a description is in the region of a connection of concepts, not in direct contact with the world of sense as is the man who says, ‘The Moon is bright’. In this respect, the distinction with which we are now concerned has a certain analogy with our previous distinction between ‘Socrates is mortal’ and ‘All Greeks are mortal’. The reader may be disposed to think that the above distinctions are mere scholastic pedantry. I must now try to explain why this is not the case.
　Source: My Philosophical Development, chap. 6：1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_06-040.HTM

　私がペアノから引き出した悟り（enlightenment 啓発/開明）は、主として二つの全く技術的な進歩から発したものであるが，私がそうであったように，算術を理解しようとして長年を過ごした後でなければ、その（技術的進歩の）重要性を認めること（appreciate 真価を認めること）は非常に困難である。この二つの進歩は、ペアノよりも前に既に G. フレーゲによって果されていたが、ペアノが当時そのことを知っていたかどうかは疑わしいし、私は少し後までその事実を知らなかった。難しい仕事であるが、私、それらの進歩が何であったか、また、なぜそれらは重要であったかについて、最善をつくして説明しなければならない。まずそれら（の進歩）が何であったか、ということから始めよう。 　最初の進歩は、「ソクラテスは死ぬものである（死ぬ運命である／不死ではない）」という形の命題を「全てのギリシャ人は死ぬものである」（注：全称命題）という形の命題から分離することで（その進歩は）成り立っていた。アリストテレスにおいては、また三段論法(注：syllogism 大前提→小前提→結論)に関する公認の学説（それをカントは永久に改善の余地はないと考えた）　においては、この二つの命題形式は区別できないものとして、あるいは,ともかくも（at any rate いずれにせよ），重要な差異がないものとしてとり扱われている。しかし、事実（実際）、論理学も数学も、この（命題の）二つの形式は全く異なったものであると理解されるまでは（理解されない限り）、遠くまで進めない（進歩できない）のである。「ソクラテスは死ぬものである」は一つの述語（注：死ぬものである）を、名付けられた（固有名をもつ）一つの主語（ソクラテス）に帰属させる。(他方)「全てのギリシャ人は死ぬものである」は、二つの述語すなわち「ギリシャ人」と「死ぬもの」との関係を言いあらわしている。（つまり）「全てのギリシャ人は死ぬものである」を、完全な形で言いあらわすと、「ｘ のあらゆる可能な値について、もし x がギリシャ人であるならば、x 死ぬものである」となる（注：従って「ギリシア人」は主語ではない！）。ここには、主語-述語命題ではなく、二つの命題関数（函数）の結合があるのであり、これら命題関数の各々は、変項 x に一つの値が与えられると（assigned to 指定されると/割り当てられると）一つの主語-述語命題となるのである。（即ち）「全てのギリシャ人は死ぬものである」という陳述（文）は、特にギリシャ人（全体）について何ごとかを言っているのでなく、宇宙の全てのものについての一つの陳述なのである。（注：x は宇宙全体を対象にしている。）「もし x がギリシャ人であるならば、x は死ぬものである」という陳述は、x がギリシャ人でない場合も、x がギリシャ人である場合と全く同様に、真である。実際、ギリシャ人というものがまったく存在しなくとも真である。たとえば、リリパット国人（Lilliputians）は存在しないが、「全てのリリパット国人は死ぬものである」という命題は真である（注：偽であることを証明するためには、リリパット人で死んだ例を１つでよいので、例を示さなければならない）。「全てのギリシャ人は死ぬものである」という陳述（文）は、「ソクラテスは死ぬものである」という陳述（文）とは異なり、いかなるものにも固有名を与えておらず（名付けておらず）、単に、二つの述語の結合を言いあらわしている（表現している）だけである。この命題は、枚挙（enumeration 単純枚挙/列挙）によっては証明できない。なぜなら（to repeat 繰り返しになるが）問題になっている x は、ギリシャ人であるところの x に限定されず、広く全宇宙のものを指しているからである。しかし、それは（単純）枚挙によって証明されないにせよ、やはり知られうるものである。私は翼がある馬が存在するかどうかを知らず、まったくそんなものに出会ったことはないが、それにもかかわらず、私は全ての翼のある馬が馬であることを知ることができる。要するに（in short）、「全ての」という語を含むあらゆる陳述は、命題関数を含むものであるが、それらの命題関数の任意の（何らかの）個別的な値を含むものではないのである。

Chapter 6: Logical Technique in Mathematics, n.3
The enlightenment that I derived from Peano came mainly from two purely technical advances of which it is very difficult to appreciate the importance unless one has (as I had) spent years in trying to understand arithmetic. Both these advances had been made at an earlier date by Frege, but I doubt whether Peano knew this, and I did not know it until somewhat later. Although it is difficult, I must do my best to explain what these advances were and why they were important. I will begin with what they were. The first advance consisted in separating propositions of the form ‘Socrates is mortal’ from propositions of the form ‘All Greeks are mortal’. In Aristotle and in the accepted doctrine of the syllogism (which Kant thought forever incapable of improvement), these two forms of proposition are treated as indistinguishable or, at any rate, as not differing in any important way. But, in fact, neither logic nor arithmetic can get far until the two forms have been seen to be completely different. ‘Socrates is mortal’ attributes a predicate to a subject which is named. ‘All Greeks are mortal’ expresses a relation of two predicates – viz. ‘Greek’ and ‘mortal’. The full statement of ‘All Greeks are mortal’ is ‘For all possible values of x, if x is Greek, x is mortal’. We have here, instead of a subject-predicate proposition, a connection of two propositional functions, each of which becomes a subject-predicate proposition when a value is assigned to the variable x. The statement, ‘All Greeks are mortal’, says nothing about Greeks in particular, but is a statement about everything in the universe. The statement ‘if x is Greek, x is mortal’ is just as true when x is not Greek as when x is Greek. Indeed, it is true if there are no Greeks at all. “All Lilliputians are mortal’ is true, although there are no Lilliputians. The statement, ‘All Greeks are mortal’, unlike the statement, ‘Socrates is mortal’, names no one and expresses only and solely a connection of predicates. It cannot be proved by enumeration, since (to repeat) the x in question is not confined to the x’s that are Greeks, but extends over the whole universe. But, although it cannot be proved by enumeration, it can nevertheless be known. I do not know whether there are any winged horses, and certainly I have never come across one, but nevertheless I can know that all winged horses are horses. In short, every statement containing the word all involves propositional functions, but does not involve any particular value of these functions.
　Source: My Philosophical Development, chap. 6：1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_06-030.HTM

　数理論理学（数学的論理学）は、決して新しい研究主題（主題分野）ではなかった。すでにライプニッツはそれを幾分試みたが、アリストテレスに対する尊敬によってさまたげられていた。G. ブール(George Boole, 1815- 1864)は1854年に『思考の法則』を出版し、集合の包含関係（class-inclusion）を主として扱う算法(calculus)の全体を展開していた。またパース(Charles Sanders Peirce、1839-1914)は、関係の論理学を展開し、シュレーダーは、それまでになした全ての仕事（研究）を要約する３巻の大著を出していた。ホワイトヘッド(Alfred North Whitehead、1861-1947)は、彼の『普遍的代数学』の最初の部分をブールの算法に捧げた(＝論じた)。以上の著作のたいていのものを私はすでによく知っていたが、私はそれらが算術の文法について何らかの新しい光（証明）をあてる（投げかける）とは認めていなかった。私は今でも、パリ（の国際哲学会議）ヘ行く直前にこの間題について私の書いた原稿をもっているが、今再読してみると、算術が論理学に提出する多くの問題の解決の糸口すらつかんでいないことがわかる。

Chapter 6: Logical Technique in Mathematics, n.2 Mathematical logic was by no means a new subject. Leibniz had made some attempts at it, but had been thwarted by respect for Aristotle. Boole had published his Laws of Thought in 1854 and had developed a whole calculus dealing mainly with class-inclusion. Pierce had developed a logic of relations, and Schreider had published a work in three big volumes summarizing all that had previously been done. Whitehead devoted the first portion of his Universal Algebra to Boole’s calculus. Most of the above works were already familiar to me, but I had not found that they threw any light on the grammar of arithmetic. I still have the MS. of what I wrote on this subject just before my visit to Paris and I find, on re-reading it, that it does not make even a beginning of solving the problems which arithmetic presents to logic.
　Source: My Philosophical Development, chap. 6：1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_06-020.HTM

　大学を(種々の)部門に分けること（faculties 学部や学科）は必要だと思うが、，それによっていくつかの非常に不幸な結果を生んできた。（たとえば）論理学は哲学の一部門と考えられており，アリストテレスによって取り扱われたために、ギリシャ語に堪能な者によってのみ取り扱われる学科（主題）だと考えられてきた。数学は、その結果として、論理学を知らない者によってのみ扱われてきた。アリストテレスやユークリッドの時代から今世紀に至るまで、論理学と数学とのこの分離は、ひどい結果を引き起こしてきた。数学の哲学にとって論理学の改革が重要であることに私が気づいたのは、1900年、パリで開かれた国際哲学会においてであった。私がそのことに気づいたのは、トリノ大学のペアノ(Turin 英 = Torino 伊)とそこに集まった他の哲学者たちとの議論を聞いたことによってであった。私はそれ以前には、ペアノの著書を知らなかった。けれどもあらゆる議論において、ペアノが他の誰よりも正確さと論理的厳格さとを示したという事実から、私は強い印象を受けた。私はベアノのところに行って,こう言った、「私はあなたの書物をすべて読みたい。複本（copies）お持ちでしょうか?」　からは持っていた。そうして、私はすぐにそれらの本を全て読んだ。数学の原理についての私自身の見解を推し進める力を与えたものはこれらのペアノの著書であった。

Chapter 6: Logical Technique in Mathematics, n.1 The division of universities into faculties is, I suppose, necessary, but it has had some very unfortunate consequences. Logic, being considered to be a branch of philosophy and having been treated by Aristotle, has been considered to be a subject only to be treated by those who are proficient in Greek. Mathematics, as a consequence, has only been treated by those who knew no logic. From the time of Aristotle and Euclid to the present century, this divorce has been disastrous. It was at the International Congress of Philosophy in Paris in the year 1900 that I became aware of the importance of logical reform for the philosophy of mathematics. It was through hearing discussions between Peano of Turin and the other assembled philosophers that I became aware of this. I had not previously known his work, but I was impressed by the fact that, in every discussion, he showed more precision and more logical rigour than was shown by anybody else. I went to him and said, ‘I wish to read all your works. Have you got copies with you?’ He had, and I immediately read them all. It was they that gave the impetus to my own views on the principles of mathematics.
　Source: My Philosophical Development, chap. 6：1959．
　More info.:https://russell-j.com/beginner/BR_MPD_06-010.HTM

　そういった（哲学に取り組み始めた）初期の時代以来、私は多様な問題について自分の意見を変えてきたけれども、現在同様当時、最重要だと思われた（いくつかの）点については（今にいたるまで）意見を変えてこなかった。私は今でも(still いまだ)、外的関係の学説(外的関係説)と，それと結びついている多元論（注：一元論に対立する考え方）とに固執している（hold to を固く信じている）。私は今でも、ひとつの孤立した真理が完全な意味で真でありうる、と信じている（注：部分的な真は本当の真ではなく、全体的な真のみが本当の真であるというヘーゲル的な考えたかに対抗する考え方）。私は今でも、分析は、ものをゆがめて見ること（falsification 歪曲/偽証）にはならない、と信じている（注：分析は部分しか見ていないので方法論として誤っているという批判に対する反論）。私は今でも(いまだ)、トートロジー（論理的真理）以外のいかなる命題も、もし仮にそれが真であるならば、事実への関係(注；事実の裏付けがあること)によって（in virtue of）真であるということ、また事実一般は経験から独立しているものである，と信じている。私は経験を欠いている宇宙（注；人間等の感覚器官を持っている生命体のいない宇宙など）において、不可能なものは何物も認めない（注：see nothing 何物も目に入らない）。反対に、経験は、宇宙の非常に小さな部分の、極めて狭く宇宙的には取るに足らない面（様相）であると考ぇる。これらすべての事柄（問題）に関して、カントとヘーゲルの教えを捨てて以来、私の見解は変わっていない（have not changed 変わってこなかった）。

Chapter 5: Revolt into Pluralism, n.17
Although I have changed my opinion on various matters since those early days, I have not changed on points which, then as now, seemed of most importance. I still hold to the doctrine of external relations and to pluralism, which is bound up with it. I still hold that an isolated truth may be quite true. I still hold that analysis is not falsification. I still hold that any proposition other than a tautology, if it is true, is true in virtue of a relation to fact, and that facts in general are independent of experience. I see nothing impossible in a universe devoid of experience. On the contrary, I think that experience is a very restricted and cosmically trivial aspect of a very tiny portion of the universe. On all these matters my views have not changed since I abandoned the teachings of Kant and Hegel.
　Source: My Philosophical Development, chap. 5：1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_05-170.HTM　　　　

　新しい哲学を展開しつつあった初期の時期において、私は、主として言語上の諸問題に非常に専念した。私は、複合体/複合物を統一するものについて(注：いくつかのもので成っているものを一つの統一体にするものについて)、特に（more especially とりわけ）ひとつの文を統一するものについて、関心を持っていた（注：単語の集まりである一つの文を一体のものとして統合化するものは何か？）。（たとえば）一つの文と一つの語（単語）との違いが（何であるか）私を困惑させた（悩ませた／難問であった）。私は文の統一が、文が動詞を含むという事実に依存している（よっている）と理解した（I saw）。しかし,私には、動詞は －－動名詞はもはや複合体の諸部分を結び合わせる能力をもたないけれども－－ それに対応する動名詞（注：verbal noun 動詞的名詞）が意味するものと全く同じことを意味するように思われた。（注：たとえば、一つの文「Brutus killed Caesar.」は一つの統一のある文であるが、Bruths; killed; Caesar の語がめちゃめちゃの順番で並んでいると意味がなくなったり、意味が変わったりする。Caear killed Brutus. にすると意味が逆になってしまう。”kill”は前後の単語を結びつける力を持っているが、”killing”というように動名詞にすると前後を一体化する力を失う。）　私は「ある」（is）と「あること」（being）との相違について思い悩んだ。有名で気力に溢れた宗教的指導者であった義母（私の妻の母）は、哲学が難しいのはただ哲学が長い語（単語）を用いるからだと私に向って自信をもって主張した。私は、その日(当日)書きつけた覚え書きの中から、次の文（一文）を示して、彼女と対峙した（confronted her with）。その文は「“is (ある)の意味するものは is（ある）であり、従って、is (ある)の意味するものは is あるとは異なる。というのは（もし同一だとすると）”is is”（あるはある）はナンセンスであろうからである。あるの意味するものはある』、と言う代りに、『あるはある』と言えるはずだが〕、『あるはある』と言うのは無意味であろうから」（What is means is and therefore differs from is, for “is is” would be nonsense.) この文が難しいのは長い単語のせいであると言うことはできない。時が経つにつれて、私はそういった問題で悩まなくなった。そういう問題は、びとつの語が何らかの意味をもつ場合には、その語の意味する何ものかが存在しなければならない、という信念から生じたものである。1905年に私が到達した「記述の理論」は、上の信念が誤まっていることを明らかにし、他のやり方では解決不可能な問題の多くを一掃した。
Chapter 5: Revolt into Pluralism, n.16 I was very much occupied, in the early days of developing the new philosophy, by questions which were largely linguistic. I was concerned with what makes the unity of a complex, and, more especially, the unity of a sentence. The difference between a sentence and a word puzzled me. I saw that the unity of a sentence depends upon the fact that it contains a verb, but it seemed to me that the verb means exactly the same thing as the corresponding verbal noun, although the verbal noun no longer possesses the capacity of binding together the parts of the complex. I worried about the difference between is and being. My mother-in-law, a famous and forceful religious leader, assured me that philosophy is only difficult because of the long words that it uses. I confronted her with the following sentence from notes I had made that day: ‘What is means is and therefore differs from is, for “is is” would be nonsense.’ It cannot be said that it is long words that make this sentence difficult. As time went on, I ceased to be troubled by such problems. They arose from the belief that, if a word means something, there must be some thing that it means. The theory of descriptions which I arrived at in 1905 showed that this was a mistake and swept away a host of otherwise insoluble problems.
　Source: My Philosophical Development, chap. 5：1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_05-160.HTM

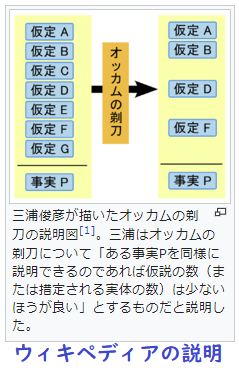
　時が経過するにつれて、私の（想定する）宇宙はそれほど豊かでなくなって行った。ヘーゲルに反逆した当初は、もの（a thing）は存在できないというヘーゲルの証明が妥当でない場合には、ものは(当然)存在しなければならない、と私は信じた。（しかし）徐々に,オッカムの剃刀(注：「ある事柄を説明するためには、必要以上に多くを仮定するべきでない」とする格言／仮定は少なければ少ないほどよい)が、もっと綺麗に剃られた実在の姿を私に与えてくれた。(ただし)オッカムの剃刀が不必要であることを示した存在者(entities)が実在しないことを証明できた,と私は言うつもりほない。私はただ,オッカムの剃刀がそれら存在者を支持する議論を消滅させたと言っているだけである。私は今でも整数や点や瞬間やオリンボスの神々が実在しないことを証明することは不可能であると考えている。ひょっとすると（For aught I know）それらは全て、実在するかも知れないが、そう考えるべきかすかな理由もないのである。

Chapter 5: Revolt into Pluralism, n.15
As time went on, my universe became less luxuriant. In my first rebellion against Hegel, I believed that a thing must exist if Hegel’s proof that it cannot is invalid. Gradually, Occam’s razor gave me a more clean-shaven picture of reality. I do not mean that it could prove the non-reality of entities which it showed to be unnecessary; I mean only that it abolished arguments in favour of their reality, I still think it impossible to disprove the existence of integers or points or instants or the Gods of Olympus. For aught I know these may all be real, but there is not the faintest reason to think so.
　Source: My Philosophical Development, chap. 5：1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_05-150.HTM

＜7月22,23日は振替休日のため、投稿を休止します。＞

　ヘーゲル主義者たちは、あれやこれやが「実在的」ではないことを証明しょうとする様々な議論（論証）を持っていた（持ち合わせていた）。数や空間や時間や物質は、すべて自己矛盾的であるということで，公然と（professedly）有罪判決を受けた（注：それらのものは「実在しない」と断罪された）。絶対者(神)以外は何ものも実在しないと、そのように我々は説得させられた。絶対者（神）は、それが他に考えるぺきものをもたずただ自己についてのみ考えうるだけであり、観念論哲学者たちが彼らの著書において考えたようなことを永遠に考えてきたのである。 　ヘーゲル主義者たちが、数学や物理学によって扱われるものを非実在的であると有罪判決を下すために用いた議論（論証）は、全て内的関係の公理(内的関係説)に依拠していた。従って、私がこの公理をしりぞけたとき、私はへーゲル主義者たちが信じなかった全てのことを信じ始めた。これは私に非常に充実した宇宙を与えた（＝物質が充満した宇宙）。私はあらゆる数がプラトン的天国で一列に並んで坐っている姿を想像した〔原注：私の(小説)『著名人の悪夢』の中の「数学者の悪夢」を参照）〕。私はまた、空間の（における）点や時間の（における）瞬間が、現実に存在しており、物質は物理学が（想定するのが）便利（都合がよい）と見出した実在の諸要素から構成されている可能性が非常に高い（might very well）、と考えた。私は大部分が動詞や前置詞によって意味されるもの（訳注：本書第14章で具体例が示されています。）で構成されてる普遍者の世界の存在を信じた。特に私は、数学が完全な意味では真ではない(not quite true)などともはや考える必要がなかった。ヘーゲル主義者たちは、２に２を加える（足すと）と４になるということは完全な意味では（完全には）真ではないと常に主張した。しかし彼らは、２に２を加えた（足した）結果は 4.000001 とかいった数であると言おうとしたのではない。彼らは実際には言わなかったけれども，言おうとしたことは、絶対者は、、加え算（足し算）などをするよりも、その心を向けるのにもっと良いものを見つけることができるということであった。しかし彼らはそのことをこのように単純な言葉で言い表わすのを好まなかったのである。

Chapter 5: Revolt into Pluralism, n.14 Hegelians had all kinds of arguments to prove this or that not ‘real’. Number, space, time, matter, were all professedly convicted of being self-contradictory. Nothing was real, so we were assured, except the Absolute, which could think only of itself since there was nothing else for it to think of and which thought eternally the sort of things that idealist philosophers thought in their books. All the arguments used by Hegelians to condemn the sort of things dealt with by mathematics and physics depended upon the axiom of internal relations. Consequently, when I rejected this axiom, I began to believe everything the Hegelians disbelieved. This gave me a very full universe. I imagined all the numbers sitting in a row in a Platonic heaven. [“Cf. my Nightmares of Eminent Persons, “The Mathematician’s Nightmare”.] I thought that points of space and instants of time were actually existing entities, and that matter might very well be composed of actual elements such as physics found convenient. I believed in a world of universals, consisting mostly of what is meant by verbs and prepositions. Above all, I no longer had to think that mathematics is not quite true. Hegelians always maintained that it is not quite true that two and two are four, but they did not mean by this that two and two are 4.000001 or some such figure. What they did mean, though not what they said, was that the Absolute can find better things to occupy its mind than doing sums, but they did not like to put the matter in such simple language.
　Source: My Philosophical Development, chap. 5：1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_05-140.HTM