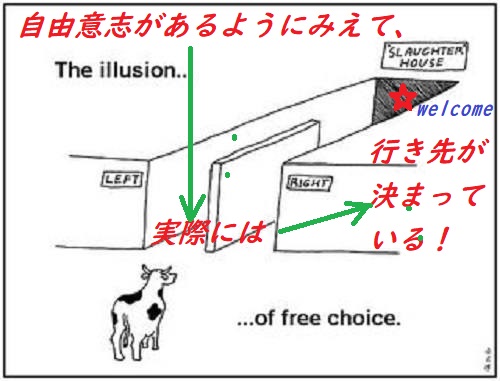
自由意志（の存在）を信ずる者は常に，他の精神領域においても，意欲（volition）には原因があると,同時に信ずる，例えば，彼ら（そう信じている人たち）は徳(美徳)は良い躾によって教え込むことができ，宗教教育は道徳にとってとても有益であると考える。彼らは説教は有益であり，道徳的奨励は多分役に立つだろう信じる。であるからには（now），もし道徳的意欲に原因がないとすれば，我々は道徳的意欲を促進することは何であれ何もできないということは明らかである。他人の望ましい行為を促進することが，自分の力の範囲内あるいは任意の誰かの力の範囲内にあると信ずる程度まで，その程度まで人は心理的因果作用（psychological causation）を信じているのであり，自由意志(の存在)を信じているわけではない。実際，我々がお互いにやることの全ては，人間の行為は（その行為に）先行する状況から生ずるという仮定に基礎をおいている。政治的宣伝，刑法，あれやこれやの行動を促す本を執筆することは，もしそれらが人の行為にまったく影響を与えないのならその存在理由を失ってしまうだろう。自由意志の教義の意味するところはそれを主張する人々に理解されていない。我々は「なぜあなたはそうしたのか？」と問い，その行為を引き起こした信念や欲求に言及する答えを期待する。ある人がなぜ自分がそのような行為をしたのかを自身でわからない場合，我々は　原因を求めてその人の無意識（の世界）を調べるかも知れない。しかし原因はまったく存在しなかったかも知れないという考えは決して心に浮かばない（生じない）。（注：荒地出版社刊の津田訳では「but it never occurs to us that there may have been no cause.」を「が原因がなかったということは決してないだろう」と誤訳している。）

Chapter 6: Determinism, n.14 Believers in free will always, in another mental compartment, believe simultaneously that volitions have causes. They think, for example, that virtue can be inculcated by a good upbringing, and that religious education is very useful to morals. They believe that sermons do good, and that moral exhortation may be beneficial. Now it is obvious that, if virtuous volitions are uncaused, we cannot do anything whatever to promote them. To the extent to which a man believes that it is in his power, or in any man’s power, to promote desirable behaviour in others, to that extent he believes in psychological causation and not in free will. In practice, the whole of our dealings with each other are based upon the assumption that men’s actions result from antecedent circumstances. Political propaganda, the criminal law, the writing of books urging this or that line of action, would all lose their raison d’etre if they had no effect upon what people do. The implications of the free-will doctrine are not realized by those who hold it. We say “why did you do it?” and expect the answer to mention beliefs and desires which caused action. When a man does not himself know why he acted as he did, we may search his unconscious for a cause, but it never occurs to us that there may have been no cause.
　出典：Religion and Science, 1935, chapt. 6:
　情報源：https://russell-j.com/beginner/RS1935_06-140.HTM

　心理学と生理学は，自由意志の問題に関する限り，自由意志（の存在）を否定する（make improbable ありそうもないものとする）傾向にある。内分泌に関する研究（work on internal secretions），脳のいろいろな部分の働きに関する知識の増加，条件反射に関するパブロフの調査研究，抑圧された記憶や欲求の及ぼす影響に関する精神分析的研究は,全て精神現象を支配する因果律（因果法則）の発見に寄与した。もちろん，これらのいずれも自由意志の（存在の）可能性を論駁（否定）しなかったが，たとえ（はっきりした）原因のない意志（uncaused volitions → 自由意志）が生じるとしても（if = even if），それらの研究は,原因のない意志（＝自由意志の存在）は非常に稀である確率を高いものとした。 　自由意志に属すると想定されている情緒的重要性は，主としてある種の思考の混乱に基づいているように思われる。人々は，もし意志に原因があるなら，自分たちがしたいとは思わないことをするように強いられるかも知れないと想像する。もちろん，これは誤り（勘違い）である。願望自体にたとえ原因があるとしても，願望は行為の原因である。我々はしたくないことをすることはできないが，そのような制約（があること）に文句を言うことは不合理だと思われる。我々の顧望が妨げられる時は不愉快であるが，願望が妨げられることは，願望に原因がない時よりも原因があるときの方がより起りそうである（可能性がある）ということはない。また，決定論は，我々は無力であるという感情を（必ず）起させることはない。権力の本質は意図した結果を得ることができるということにあり，それは，我々の意図の原因が発見されることにより増加したり減少したりしない。

Chapter 6 Determinism, n.13
Psychology and physiology, in so far as they bear upon the question of free will, tend to make it improbable. Work on internal secretions, increased knowledge of the functions of different parts of the brain, Pavlov’s investigation of conditioned reflexes, and the psycho-analytic study of the effects of repressed memories and desires, have all contributed to the discovery of causal laws governing mental phenomena. None of them, of course, have disproved the possibility of free will, but they have made it highly probable that, if uncaused volitions do ever occur, they are very rare. The emotional importance supposed to belong to free will seems to me to rest mainly upon certain confusions of thought. People imagine that, if the will has causes, they may be compelled to do things that they do not wish to do. This, of course, is a mistake ; the wish is the cause of action, even if the wish itself has causes. We cannot do what we would rather not do, but it seems unreasonable to complain of this limitation. It is unpleasant when our wishes are thwarted, but this is no more likely to happen if they are caused than if they are uncaused. Nor does determinism warrant the feeling that we are impotent. Power consists in being able to have intended effects, and this is neither increased nor diminished by the discovery of causes of our intentions.
　出典：Religion and Science, 1935, chapt. 6:
　情報源：https://russell-j.com/beginner/RS1935_06-130.HTM

　A. エディントン(Sir Arthur Stanley Eddington, 1882-1944:英国の天文学者)は，原子の自由 －それ（注：原子の行動は全て決まっているわけではないこと）を事実と仮定して－ から情緒的に受け入れることができる結論に到達するために，彼自身認めているように，現在でもまったくの仮説に過ぎない想定をすることを余儀なくされた。彼は人間の自由意志（人間に自由意志があること）を守りたいと望んでおり －自由意志が何らかの重要性を持つとしたら－ 自由意志は大規模な物体を扱う力学（large-scale mechanics （注：古典力学の中の大規模な物体を扱う部分）の法則から生ずる運動以上の大規模な身体運動（活動）を引き起こす力を持たなければならない。ところで，既に考察したように，大規模な物体を扱う力学の法則は，原子に関する新しい理論（注：量子力学）によって変更される（変更を受ける）ことはない。（即ち）唯一の相違は，（現在の）大規模力学は（従来の）確実性（の断定）のかわりに，非常に高い確率があること（overwhelming probabilities）を述べるという点である（注：大規模な物体については古典力学の法則が今でも通用するが，現代物理学からみればその法則は絶対確実なものではなく、非常に確率が高いと言うべきである､といった趣旨／ちなみに，荒地出版社刊の津田訳では，「they now state」の「they」を新理論（量子力学）として「唯一のちがいは，新理論が今日，確実性についてよりも強度の蓋然性について語る点である」と訳している。一見間違ってないように見えるかも知れない。しかし「they」は直前の文の主語「the laws of large-scale mechanics」ととるのが素直であろう。即ち，「大規模な物体を扱う力学は、量子力学出現前後で変化はなく、ただ違いは・・・にある」と解釈すべきであろう）。非常に小さな力が非常に大きな効果（effect 影響）を及ぼすかも知れないがゆえに（可能性があるために）,これらの法則の確率（蓋然性）はある種特有の不安定性によって打ち消されると想像することも可能である。エディントンはこのような不安定性が生体（living matter）に，特に脳の中に，存在するかも知れないと想像することは可能である。（注：このあたりは，人間と言えども原子の集合体であることを念頭に読む必要がある。）意志（による）行為がひとつの原子をあの選択ではなくこの選択へと導き，そのことがあるとてもデリケートなバランスをひっくりかえし，そうして，別のことではなくあることを言う（語る）というような大規模な結果を引き起こすかも知れない。このようなことは理論的には（abstractly 抽象的には)可能であることを否定できないが，しかしそれは（理論的に）承認できる（妥協できる）限界である（the most that can be conceded）。原子に（想定された／仮定された）自由を認めない新しい法則が発見されるだろうということも可能性があることであるし，また，それはより確率が高いことであると私には思われる。そうして，原子に（行動の）自由を認める場合でさえも，かなりの大きさの他の物体の運動に伝統的な力学（古典力学）を適用することを可能にしている平均化の過程を，人体の大規模な運動（動き）は免除されているという経験的証拠は存在しない。従って，人間の自由意志を物理学と調和させようとするエディントンの試みは，興味深くまた（現在のところ）厳密な意味では論駁しえないものであるが，量子力学の勃興以前に行なわれていたこの問題に関する諸理論に変更を加えることを必要とするほど十分にもっともらしいものだとは思われない。

Chapter 6: Determinism, n.12
In order to arrive at emotionally agreeable conclusions from the freedom of the atom – assuming this to be a fact – Eddington is compelled to make a supposition which, he admits, is at present no more than a bare hypothesis. He wishes to safeguard human free will, which, if it is to have any importance, must have the power of causing large-scale bodily movements other than those resulting from the laws of large-scale mechanics. Now the laws of large-scale mechanics, as we have seen, are unchanged by the new theories as to the atom ; the only difference is that they now state overwhelming probabilities instead of certainties. It is possible to imagine these probabilities counteracted by some peculiar kind of instability, owing to which a very small force might produce a very large effect. Eddington imagines that this sort of instability may exist in living matter, and more particularly in the brain. An act of volition may lead one atom to this choice rather than that, which may upset some very delicate balance and so produce a large-scale result, such as saying one thing rather than another. It cannot be denied that this is abstractly possible, but that is the most that can be conceded. It is also a possibility, and to my mind a much more probable one, that new laws will be discovered which will abolish the supposed freedom of the atom. And even granting the freedom of the atom, there is no empirical evidence that large-scale movements of human bodies are exempt from the process of averaging which makes traditional mechanics applicable to the movements of other bodies of appreciable size. Eddington’s attempt to reconcile human free will with physics, therefore, though interesting and not (at present) strictly refutable, does not seem to me sufficiently plausible to demand a change in the theories on the subject which were held before the rise of quantum mechanics.
　出典：Religion and Science, 1935, chapt. 6:
　情報源：https://russell-j.com/beginner/RS1935_06-120.HTM

　量子力学において新しいことは，統計的諸法則の出現（自体）ではなく，－個々の出来事を支配する諸法則から導きだされる代わりに－ 統計的諸法則は究極的なものであるという示唆である。これは非常に難しい概念であり，量子力学の支持者たちが理解している以上に難しい概念である，と私は考える。一つの原子が行う種々の事柄（different things）について（事柄のなかで），原子は各々一定の割合（比率）の場合（事例）においてそれぞれの事柄を行う，ということが観察されてきた。しかし，もしその単一の原子が無法則（法則に従わない）とするならば，大きな数（の原子）に関してはどうしてそのような規則性が存在しなければならないのだろうか？　稀な（原子の）遷移は何らかの通常でない環境（状況）に依存しなければならない（依存しているに違いない），と人は考えるだろう。我々は，実際にかなり身近なたとえ話をひとつしてよいだろう（take an analogy たとえ話をする）。屋内用プール（swimming-bath）には，ダイバーが好きな高さから跳び込むことができる踏み段（ステップ）がある。もしその段をとても高いところまで登れば，最上段は非常に優れたダイバーだけしか選ばないであろう。ある季節を他の季節と比べると，（踏み台の）種々の段を選ぶダイバーの割合（比率）には明らかにかなりの程度の規則性があるだろう。もしダイバーが何十億も（無数に）いれば，その規則性はより大きくなると想定してもよいだろう。しかし，もし個々のダイバーにどの踏み段を選択するかについてまったく動機がなかったとすれば，なぜこのような規則性が存在するのか理解することは困難である。正しい比率を保つために，高い踏み台を選ばなければならないダイバーが存在しているかのごとく思われる。しかしそれはもう純粋な気まぐれではないであろう（気まぐれなふるまいとは言えないであろう）。 　確率論（蓋然性の理）論は（現在）論理的にも数学的にも極めて不満足な状態にある。そうして，私は個々の場合（事例）においては単なる気まぐれであるのに（それらをただまとめた）大きな数の場合には規則性が生れるというような何らかの錬金術（alchemy）が存在するなどとは信じない。もしペニー硬貨が本当に気まぐれで表になるか表になるかを（自分で）選ぶとするならば，一方を他方と同じ位の回数（ペニー硬貨は）選ぶと主張する何らかの理由が存在するだろうか？　気まぐれが好都合に（just as well）常に同じ選択に導かないかも知れないのではないか？　これは示唆にすぎない。なぜなら，問題は漠然とし過ぎており，独断的に述べることはできないからである。しかしこの示唆が何らかの確実性を持っているとしたら，我々は世界における究極的な規則性は大きな数の事例を処理しなければならないという見解を受け容れることができず、また､我々は，原子の行動の統計的法則は，個々の原子の行動に関する未発見の法則から派生すると想定しなければならない。

Chapter 6 Determinism, n.11
What is new in quantum mechanics is not the occurrence of statistical laws, but the suggestion that they are ultimate, instead of being derived from laws governing individual occurrences. This is a very difficult conception – more difficult, I think, than its supporters realize. It has been observed that, of the different things an atom may do, it does each in a certain proportion of cases. But if the single atom is lawless, why should there be this regularity as regards large numbers? There must, one would suppose, be something that makes the rare transitions depend upon some unusual set of circumstances. We may take an analogy, which is really rather close. In a swimming-bath one finds steps which enable a diver to dive from any height that he may prefer. If the steps go up to a great height, the highest will only be chosen by divers of exceptional excellence. If you compare one season with another, there will be a fair degree of regularity in the proportion of divers who choose the different steps ; and if there were billions of divers, we may suppose the regularity would be greater. But it is difficult to see why this regularity should exist if the separate divers had no motive for their choice. It would seem as if some men must choose the high dives, in order to keep up the right proportion ; but that would no longer be pure caprice. The theory of probability is in a very unsatisfactory state, both logically and mathematically ; and I do not believe that there is any alchemy by which it can produce regularity in large numbers out of pure caprice in each single case. If the penny really chose by caprice whether to fall heads or tails, have we any reason to say that it would choose one about as often as the other? Might not caprice lead just as well always to the same choice? This is no more than a suggestion, since the subject is too obscure for dogmatic statements. But if it has any validity, we cannot accept the view that the ultimate regularities in the world have to do with large numbers of cases, and we shall have to suppose that the statistical laws of atomic behaviour are derivative from hitherto undiscovered laws of individual behaviour.
　出典：Religion and Science, 1935, chapt. 6:
　情報源：https://russell-j.com/beginner/RS1935_06-110.HTM

　このような議論（論証）によって提起されている問題（問い）は，原子とは特別な関係を持たないものであり，その問題について考える際，我々の心の中から量子力学に関するあらゆるややこしい事柄（complicated business）を放逐しても（dismiss from）よいだろう。その代りに（原子の代わりに）１ペニー硬貨を投げるというお馴染みの操作（operation）を取り上げてみよう（the familiar operation of tossing a penny）。我々はその１ペニー硬貨の回転は力学の法則によって決定されており，厳密な意味で，硬貨の表が出るか裏が出るか(heads or tails)を決めるのは「偶然」ではないと確信している（参考：EXILE / Heads or Tails (Music Video)）。しかし，その計算は我々にとってはとても複雑なので，任意の場合において，どちらが出るか（表がでるか裏が出るか）我々には分らない。もしあなたが１ペニー硬貨を非常に多くの回数投げたなら －私はこれまでその充分な実験的証拠を見たことは全くないが－ 裏が出るのと同じくらいの頻度で表が出ると言われている。さらに，このことは確実ではないが極めて起こりそうなことである（確からしい／確率が高い）とだけ言われている。あなたが１ペニー硬貨を10回投げ続けて，10回とも表が出ることもあるかも知れない。10回の硬貨投げを1024回（注：従って投げる総回数は10240回）繰り返してやり,その中で一度だけ表が10回出続けることは驚くことではないだろう。（注：荒地出版社刊の津田訳ではこの箇所はあいまいな訳になっている。）しかし，もっと何度も繰返したら，表だけが続けて出る回数はもっとずっと稀になっていく（注：言うまでもなく，そういう例は増えていくが、全体のなかでの頻度/割合は減っていくので「稀になっていく」ということ）。もしあなたが１ペニー硬貨を 1,000,000,000,000,000,000,000,000,000,000 回も投げたとしても，100回続けて表が出るのが一度得られれば、あなた運が良いであろう（注：連続1,000回表が出続けるのはもっと稀になる）。少なくとも，理論はそういうことであるが，人生は短く，それを経験的に試すことはできない。 　量子力学が発見されるずっと以前から，すでに統計的な法則は物理学において重要な役割を果していた。たとえば，気体（ガス）はあらゆる方向に多様な速度でランダムに動いている膨大な数の分子で成り立っている。（分子の）平均速度が大きい時にはその気体（ガス）は熱く，小さい時にはその気体（ガス）は冷たい。全ての分子が静止している時には気体（ガス）の温度は絶対零度である。分子は常に相互に衝突し合っているということのために，平均速度よりも速く動いている分子（衝突により）は速度が低下し，遅く動いている分子は（衝突により）速度が速まる。これが，もし異なった温度の二つの気体（ガス）が接触すれば，両方の気体が同一の温度になるまで，冷たい方（の気体）は暖かくなり，温かい方（の気体）は冷たくなる理由である。しかし，このようなことは全て起こりそうなことである（起こる確率が高い）ということに過ぎない。最初は（部屋全体に渡って）同じ温度にあった室内において，速く動く分子は全て（部屋の）一方の側に集まり，ゆっくり動く分子は全て（部屋の）反対側に集まるかも知れない。そのような場合，何らか外的な原因が働かない限り，部屋の片側は冷たくなり，部屋の反対側は暑くなる。さらに，空気の全てが部屋の一方（片側）に集まり，（部屋の）反対側の半分が空になる（気体がなくなる）ことさえ起るかも知れない。このようなことは，分子の数が秘めて大であるから，コインが100回続けて表が出ることより確率は甚だしく少ないが，厳密に言えば，不可能なことではない。

Chapter 6 Determinism, n.10
The question raised by this argument is one which has no special connection with atoms, and in considering it we may dismiss from our minds all the complicated business of quantum mechanics. Let us take instead the familiar operation of tossing a penny. We confidently believe that the spin of the penny is regulated by the laws of mechanics, and that, in the strict sense, it is not “chance” that decides whether the penny comes heads or tails. But the calculation is too complicated for us, so that we do not know which will happen in any given case. It is said (though I have never seen any good experimental evidence) that if you toss a penny a great many times, it will come heads about as often as tails. It is further said that this is not certain, but only extremely probable. You might toss a penny ten times running, and it might come heads each time. There would be nothing surprising if this happened once in 1,024 repetitions of ten tosses. But when you come to larger numbers the rarity of a continual run of heads grows much greater. If you tossed a penny 1 ,000,000,000,000,000,000,000, 000, 000,000 times, you would be lucky if you got one series of 100 heads running. Such at least is the theory, but life is too short to test it empirically. Long before quantum mechanics were invented, statistical laws already played an important part in physics. For instance, a gas consists of a vast number of molecules moving at random in all directions with varying speeds. When the average speed is great, the gas is hot ; when it is small, the gas is cold. When all the molecules stand still, the temperature of the gas is the absolute zero. Owing to the fact that the molecules are constantly bumping into each other, those that are moving faster than the average get slowed down, and those that are moving slower get speeded up. That is why, if two gases at different temperatures are in contact, the colder one gets warmer and the warmer one gets colder until they reach the same temperature. But all this is only probable. It might happen that in a room originally at an even temperature all the fast-moving particles got to one side, and all the slow-moving ones to the other ; in that case, without any outside cause, one side of the room would get cold and the other hot. It might even happen that all the air got into one half of the room and left the other half empty. This is vastly more improbable than the run of 100 heads, because the number of molecules is very great ; but it is not, strictly speaking, impossible
　出典：Religion and Science, 1935, chapt. 6:
　情報源：https://russell-j.com/beginner/RS1935_06-100.HTM

　このような議論に対し，決定論者は二つの異なったやり方で答えようとするかもしれない。 　彼は次のように論ずるかもしれない。（即ち）過去において，始めのうちは法則に従わないように思われた出来事も，後になって，ある法則に従っていたことが示されてきており，また，まだ示されていなくても，（当該）主題（subject-matter）が極めて複雑であることが充分な言いわけになる，と（注：事柄が複雑だから簡単に法則は見つからないのだという言い訳が成立する，との弁解）。多くの哲学者たちが信じてきたように，もし法則の支配を信ずることを是とするア・プリオリな（先験的な）理由が存在するとしたら（仮定したなら），それは十分な議論（論拠）となったであろう。しかし，もしそのような理由がないまったく存在しなければその議論（論拠）はとても効果的な反論にさらされる。（即ち，）大規模な出来事の規則性は，個々の原子の行動（doing なすこと）における規則性を想定する必要なしに，確率の法則（laws of probability 蓋然性の法則）から導き出される。量子力学（quantum theory 量子論）が個々の原子に関して想定しているのは確率の法則である。原子に開かれている（open to）可能な選択（肢）のなかで，第一の選択が行われる既知の確率があり，第二の選択が行われる既知の確率があり，以下同様（それぞれの選択の確率がわかっている）。この確率の法則から，大きな物体は「ほとんど」古典力学が予想したように行動することが確かであるという推測ができる（可能である）。従って，大きな物体について観察される規則性は，ただ蓋然的かつ近似的なものであり，個々の原子の行動に完全な規則性を予期するための帰納的根拠（inductive ground）をまったく与えない（のである）。 　決定論者が試みるかもしれない第二の回答はより困難なものであり，今のところ，その妥当性を評価することはほとんど不可能である。彼は次のように言うかも知れない。（即ち）外見上同じ環境にある，大量の似通った原子の選択（結果）を観察すれば，それらの原子が種々の可能な遷移をする頻度に規則性が存在している，ということをあなたは認める（だろう）。この事例は，男女の出生の事例に似ている。我々は個々の出生が男になるか女になるかはわからないが，（たとえば）大英帝国においては，男女の出生比率は男21に対し女20であることを知っている。このようにして，任意の家庭においてはそうでないとしても，全人口の性の比率には規則性が存在している。今日では，男女の誕生の場合は（事例は），個々の場合において性を決める原因があると皆信じている。我々は21対20の比率を与える統計の法則は，個々の場合にあてはまる法則の結果に違いないと考える（注：個々の赤ん坊が男か女である確率は21対20である，ということ。ちなみに男のほうが出生率が高いのに女とほぼ同数になるのは、男の赤ん坊のほうが死亡率が高いため）。同様に，もし，大量の原子に関して統計上の規則性が存在するなら，それは個々の原子の行動を規定する法則が存在するからに違いない，と論ぜられるかも知れない。そうして，もしそのような法則が存在しないなら統計上の法則もまったく存在しないだろう，と決定論者は論ずるかも知れない。

Chapter 6: Determinism, n.9
To this argument the determinist may attempt to reply in two different ways. He may argue that, in the past, occurrences which, at first, seemed not subject to law, have afterwards been shown to follow some rule, and that, where this has not yet occurred, the great complication of the subject-matter affords a sufficient explanation. If, as many philosophers have believed, there were a priori reasons for believing in the reign of law, this would be a good argument ; but if there are no such reasons, the argument is exposed to a very effective retort. The regularity of large-scale occurrences results from the laws of probability, without the need of assuming regularity in the doings of individual atoms. What quantum theory assumes as regards individual atoms is a law of probability : of the possible choices open to the atom, there is a known probability of one, another known probability of a second, and so on. Frorn this law of probability it can be inferred that large bodies are almost certain to behave as traditional mechanics expect. The observed regularity of large bodies, therefore, is only probable and approximate, and affords no inductive ground for expecting a perfect regularity in the doings of individual atoms. A second reply which the determinist may attempt is more difficult, and as yet it is scarcely possible to estimate its validity. He may say : You admit that, if you observe the choices of large numbers of similar atoms in apparently similar circumstances, there is regularity in the frequency with which they make the various possible transitions. The case is similar to that of male and female births ; we do not know whether a particular birth will be male or female, but we know that, in Great Britain, there are about 21 male births for every 20 female births. Thus there is regularity in the proportion of the sexes throughout the population, though not necessarily in any one family. Now in the case of male and female births everybody believes that there are causes which determine sex in each separate case ; we think that the statistical law giving the proportion of 21 to 20 must be a consequence of laws which apply to individual cases. In like manner, it may be argued, if there are statistical regularities where large numbers of atoms are concerned, that must be because there are laws which determine what each separate atom will do. If there were not such laws, the determinist may argue, there would be no statistical laws either.
　出典：Religion and Science, 1935, chapt. 6:
　情報源：https://russell-j.com/beginner/RS1935_06-090.HTM

　決定論者にとって不運なことに，原子の気まぐれ（不確定性）に関する現代の理論にはさらなる一歩前進があった。我々は，物体（bodies）が常にその動きを完全に決定する法則に従って運動することを証明する傾向のある,大量の証拠を一般物理学（注：ordinary physics：量子力学や相対性理論のような現代物理学ではない，従来の古典物理学のことか）は持っていた－あるいは持っていると考えていた。今日では，これらの法則はみな単に統計的なものにすぎないだろうと思われている。原子は一定の比率で（多くの）可能性の中で選択を行う。そうして原子はとても膨大な数があり，（選択の）結果は －旧来の方法で充分観察されるほど十分に大きな物体に関しては－，完全な規則性を持つという外見（様子）をしている（注：have the appearance of 様子をする/外見を持つ）。（たとえば）あなたは，個々人を見ることができないほどの巨人であり，百万人の個人の集団でないと気づかないと想定してみよう。すると，あなたは，(数百万の人口を持つ)ロンドン（注：ロンドンは当時世界最大の都市であり，1901年には約650万，1939年には約860万人までに増加した。）は夜間よりも昼間により多くの物体（物質/もの）を含むという程度のことに気付くことはできるだろうが，しかし，多分，ある日ディクソン氏は具合が悪くなって床に伏したために彼はいつもの汽車には乗らなかったという事実にはあなたは気付かないだろう。従って，あなたは，朝ロンドンに流れ込み，夕方そこから出てゆく物体（物質）の運動を，実際以上（than it is）に規則的な出来事（affair)であると信ずるだろう。あなたは疑いもなく（ロンドンの）霧深い気候の中では運動が遅滞するという観察によって確証される仮説を，太陽の中にあるある特殊な力に帰するだろう。もし，後にあなたが個々の人間を観察できるようになった時には，あなたが（以前）考えていたほどの規則性はないことを発見するだろう。（たとえば）ある日にはディクソソ氏が病気になり，別の日にはシンプソン氏が病気になる。（だれが病気になろうと）統計的な平均は影響されない（注：病気になる確率は変わらない）。大規模な観察の場合は違いはない（差は生じない）。あなたが以前に観察した全ての規則性はデイクソン氏やシンプソン氏が朝ロンドンへたまたま行かなかったことに気まぐれ以上の何かの理由（注：病気だった）があったと想定しなくても，統計学の大数の法則（laws of large numbers）によって説明されることが分るだろう。これがまさに物理学が原子に関して（現在）到達している状況である。物理学は原子の行動(運動)を完全に決定するいかなる法則も知らない。そうして物理学が発見した統計学的法則は大きな物体の運動において観察された規則性に対する説明としてはそれで十分である。そうして，決定論を是とする主張はこれらの大きな物体の運動に依拠していたものであったので，その論拠は破たんしたように思われる。

Chapter 6: Determinism, n.8
Unfortunately for the determinists, there is a further step in the modern doctrine of atomic caprice. We had – or so we thought – a great mass of evidence from ordinary physics, tending to prove that bodies always move in accordance with laws which completely determine what they will do. It now appears that all these laws may be merely statistical. The atoms choose among possibilities in certain proportions, and they are so numerous that the result, as regards bodies large enough to be observed by old-fashioned methods, has an appearance of complete regularity. Suppose you were a giant who could not see individual men, and never became aware of an aggregate of less than a million of them. You would just be able to notice that London contains more matter by day than by night, but you could not possibly be aware of the fact that, on a given day, Mr. Dixon was ill in bed and did not take his usual train. You would therefore believe the movement of matter into London in the morning and out of it in the evening to be a much more regular affair than it is. You would no doubt attribute it to some peculiar force in the sun, a hypothesis which would be confirmed by the observation that the movement is retarded in foggy weather. If, later, you became able to observe individual men, you would find that there is less regularity than you had supposed. One day Mr. Dixon is ill, and another, Mr. Simpson ; the statistical average is not affected, and to large-scale observation there is no difference. You would find that all the regularity you had previously observed could be accounted for by the statistical law of large numbers, without supposing that Mr. Dixon and Mr. Simpson had any reason beyond caprice for their occasional failure to go to London in the morning. This is exactly the situation at which physics has arrived in regard to atoms. It does not know of any laws completely determining their behaviour, and the statistical laws which it has discovered are sufficient to account for the observed regularity in the motions of large bodies ; and as the case for determinism has rested on these, it seems to have broken down.
　出典：Religion and Science, 1935, chapt. 6:
　情報源：https://russell-j.com/beginner/RS1935_06-080.HTM

　量子力学によると，原子が一定の状況において何をするか（＝どのような動きをするかまたどのような変化をするか）（我々は）知ることはできない。原子には（可能性として）開かれている一定の範囲の選択肢（a definite set of alternatives ）が存在しており，時にはある選択肢を，また時には別の選択肢を選ぶ。我々は，どのような比率の事例で一つの撰択がなされ，どのような比率の事例で２番めの選択が，さらにどのような比率の事例で３番めの選択がなされるか等々，について知っている。しかし，個々の実例における選択を決定する法則については，我々はまったく何も知らない。我々は（ロンドンの）バディントン駅の切符売り場の係員（booking-office clerk）と同じ立場にある。彼はその気になりさえすれば，パディントン駅からバーミンガム駅へ，パディントン駅からエクセター駅へ、また，パディントン駅からその他の駅へ,向かう旅行者の割合について知ることができるが，ある場合にある選択を行い、別の場合には別の選択を行うにいたった個々の理由については何も知らない。けれども，これらの事例は（物理学者の事例と切符売りの事例とは）「完全に」類似しているわけではいない。なぜなら，切符売りは，仕事以外の時（moments 瞬間，機会)を持っており，その時には，切符を扱っている時には彼らが言及しないような,人間に関するいろいろなことを発見できるからである。物理学者にはそういった利点（advantage 長所）はない。なぜなら，彼（物理学者）は仕事をしていない時には原子を観察する機会はまったくないからである。彼は，実験室にいない時には，何百万もの原子から成り立っている大きな塊（注：large masses 分子でできているもの；大きな質量）によってなされることを観察可能なだけである。そうして，（原子を観察できる）実験室においても，原子は，汽車が発車直前に急いで切符を受け取る人々（乗車客）よりも話しかけることができるということはほとんどありえない。従って，物理学者の（原子の行動に関する）知識は，切符売りが勤務時間外に常に居眠りしていた場合（時）の知識のようなものであろう。 　これまでのところ，原子の行動から導き出される,決定論に反対する議論（論拠）は，ほとんど我々の現時点での無知に基づいており，また新法則の発見によって近い将来（to-morrow = tomorrow）反駁されるかも知れない，と思われるかも知れない(it might seem that)。ある点まで,，それは真実である。原子に関する我々の詳細な知識はごく最近のものであり，それは今後増すだろうと考える充分な理由がある。どうして,一つの原子がある瞬間にある一つの可能性を選択し，他の瞬間には他の可能性を選択する理由を示す法則が発見されるかも知れない，ということを誰も否定できない。現在のところ，我々は二つの異なった選択がなされる先行（状態）(antecedent 前件；先立つもの，先行するもの)の相違について何も知らないが，何時かそのような相違が見出されるかも知れない。もし，我々が決定論を信ずる何らこの強力な理由を持つとしたら，この議論（論拠）は重要な役割を果たすであろう。（If we had any strong reason to believe in determinism,仮定法）

Chapter 6: Determinism, n.7
According to quantum mechanics, it cannot be known what an atom will do in given circumstances ; there are a definite set of alternatives open to it, and it chooses sometimes one, sometimes another. We know in what proportion of cases one choice will be made, in what proportion a second, or a third, and so on. But we do not know any law determining the choice in an individual instance. We are in the same position as a booking-office clerk at Paddington, who can discover, if he chooses, what proportion of travellers from that station go to Birmingham, what proportion to Exeter, and so on, but knows nothing of the individual reasons which lead to one choice in one case and another in another. The cases are, however, not wholly analogous, because the booking-office clerk has his non-professional moments, during which he can find out things about human beings which they do not mention when they are taking tickets. The physicist has no such advantage, because in his unprofessional moments he has no chance to observe atoms ; when he is not in his laboratory, he can only observe what is done by large masses, consisting of many millions of atoms. And in his laboratory the atoms are scarcely more communicative than the people who take tickets in a hurry just before the train starts. His knowledge, therefore, is such as the booking-office clerk’s would be if he were always asleep except in working hours. So far, it might seem that the argument against determinism derived from the behaviour of atoms rests wholly on our present ignorance, and may be refuted to-morrow by the discovery of a new law. Up to a point, this is true. Our detailed knowledge of atoms is very recent, and there is every reason to suppose that it will increase. No one can deny that laws may be discovered which will show why an atom chooses one possibility on one occasion and another on another. At present, we know of no relevant difference in the antecedents of the two different choices, but some such difference may be found any day. If we had any strong reason to believe in determinism this argument would carry great weight.
　出典：Religion and Science, 1935, chapt. 6:
　情報源：https://russell-j.com/beginner/RS1935_06-070.HTM

　それゆえ，陳述（statement）がいくらか複雑ではないかと恐れるが，今や我々は，決定論の仮説を述べることが出来る。その仮説は以下のとおりである。 「十分な（しかし超人的でない）計算能力が与えられさえすれば，ある一定の領域内で起こっている全てのことを知っている人間が，その領域の境界からその領域の中心まで光が進むのに要する時間（内）に起るであろうことを予言できるような，発見可能な因果律（因果法則）が存在する。」 　私がこの原理（説）を真理であると主張しているのではないことははっきり理解していただきたい。私はただ，もし「決定論」を是（正しい）とするあるいは非（間違っている）とする証拠が何か存在しなければならないとするならば，この原理こそ「決定論」という言葉が意味すべきことであると主張しているだけである。私はこの原理が真理であるかどうか知らない。また私以外の誰も知っていない。それは，これは科学が自らの前に抱くひとつの理想とみなされるかも知れないが，しかし，何らかの「先験的な（a priori）」根拠にのとってということでなければ，確実に真理とも虚偽とも見なすことはできない。おそらく，我々が決定論を肯定あるいは否定する議論（論拠）を吟味すると，人々が心に抱いていたものは，我々が到達した原理（注：上述）よりもどちらかというと明確でないものであったということを発見するであろう。 　史上初めて，決定論は,今日,科学者から科学的根拠に基づく挑戦を受けている。その挑戦は，量子力学の新しい方法による原子の研究を通して成し遂げられてきている（has come through）。この攻撃の指導者は（これまで）アーサー・エディントン卿であり，最良の物理学者たちの何人か（例えばアインシュタイン）は，この問題に関する彼の見解に同意していないが，彼の議論（論拠）は強力であり，我々はそれをできるだけ専門技術的な言葉を使わずに（without technicalities）吟味しなければならない。

Chapter 6: Determinism, n.6
We can therefore now state the hypothesis of determinism, though I am afraid the statement is rather complicated. The hypothesis is as follows ; There are discoverable causal laws such that, given sufficient (but not superhuman) powers of calculation, a man who knows all that is happening within a certain sphere at a certain time can predict all that will happen at the centre of the sphere during the time that it takes light to travel from the circumference of the sphere to the centre. I want it to be clearly understood that I am not asserting this principle to be true ; I am only asserting that it is what must be meant by “determinism” if there is to be any evidence either for or against it. I do not know whether the principle is true, and no more does anybody else. It may be regarded as an ideal which science has held before itself, but it cannot be regarded, unless on some a priori ground, as either certainly true or certainly false. Perhaps, when we come to examine the arguments that have been used for and against determinism, we shall find that what people have had in mind was something rather less definite than the principle at which we have arrived. For the first time in history, determinism is now being challenged by men of science on scientific grounds. The challenge has come through the study of the atom by the new methods of quantum mechanics. The leader of the attack has been Sir Arthur Eddington, and although some of the best physicists (e.g. Einstein) do not agree with his views on this matter, his argument is a powerful one, and we must examine it as far as is possible without technicalities.
　出典：Religion and Science, 1935, chapt. 6:
　情報源：https://russell-j.com/beginner/RS1935_06-060.HTM

　我々は次のような方法でこのような困難から脱出を試みることできる。我々は，我々がその中心を占めている(中心にいる)ある領域内で1936年（注：ラッセルのこの本の出版の翌年）始めに起こりつつある全てのことを知っていると仮定(想定)してみよう。物事を明確にするために,(とりあげる)その領域は極めて広大で，光がその領域の境界線（注：circumference その領域の中心から一番離れたところ）からその領域の中心に到達するのにちょうど一年かかるとしよう（注：つまり１光年の範囲）。その場合（Then），光よりも早く動くものはないから，1936年にその領域の中心で起る全てのことは －決定論が正しければ－ その年（1936年）の始めにその領域の中に存在したことにのみ依存しなければならない。なぜなら，それより遠くにある物は，その領域の中心に何らかの影響を持つのに一年以上かかるであろうからである（注：荒地出版社刊の津田訳では「a certain sphere」を「ある領域」と訳し，そのすぐ後の「the sphere」を「天体」と訳しているので，前者と後者が同じ領域のことを言っていると理解できない訳し方となっている）。我々は，実際，その年（1936年）が終るまで想定されているデータ（our supposed data 我々が想定しているデータ）を全部入手することはできないだろう。なぜなら，（１光年先の）周辺領域から我々のところに（光が）達するにはそれだけの長さの時間かかるだろうからである。しかし，その年が終ると，時間を遡って，我々がいま持っているデータが，既知の因果律（因果法則）とともに（と一緒に），その年（1936）に地球上で起こった全てのことを説明する（account for 釈明する）かどうかを調査することができる。

Chapter 6: Determinism, n.5
We can attempt to escape from this difficulty in the following manner. Let us suppose that we know everything that is happening at the beginning of 1936 within a certain sphere of which we occupy the centre. We will assume, for the sake of definiteness, that the sphere is so large that it takes just a year for light to travel from the circumference to the centre. Then, since nothing travels faster than light, everything that happens at the centre of the sphere during the year 1936 must, if determinism is true, be dependent only on what was inside the sphere at the beginning of the year, since more distant things would take more than a year to have any effect at the centre. We shall not really be able to have all our supposed data till the year is over, because it will take that length of time for light to reach us from the circumference ; but when the year is over we can investigate, retrospectively, whether the data we now have, together with known causal laws, account for everything that happened on the earth during the year.
　出典：Religion and Science, 1935, chapt. 6:
　情報源：https://russell-j.com/beginner/RS1935_06-050.HTM