（続き）さて内面的関係の公理の意味とそれに対する賛否の理由(根拠)についてもっと入念に（closely）考察してみよう。まず、全ての関係がその諸項の本性（性質）によってまたは諸項が構成する全体の本性（性質）によって実際に（本当に）構成されると考えるか、あるいは、全ての関係は単にそれらの諸項の本性（性質）の中に（ひとつの）基礎を持っているだけであると考えるか、のいずれで考えるかに従って、（内面的関係説には）二つの意味がありうる（が可能である）。（しかし）観念論者たちがこれらの二つの意味を区別しているとは私には認められない（I do not observed that idealists distinguish ~：区別しているのを見た（観察した／気づいた）ことがない）。実際、一般的にいって（大雑把に言って）、彼ら（内面的関係説の立場の哲学者たち）は，（一つの）命題とその命題の帰結とを同一視する傾向があり、そうしてプラグマティズム（実用主義）の顕著な信条の一つを具現化している。けれども、内（面的関係説における）二つの意味を区別することは、－－それは、この後で見るように、関係というものは（そもそも）全く存在しないという見解に導くので－－ ２つの意味を区別しない場合に比べて、重要性がより少ない。（注：とまり、2つの意味を区別しないことは大きな問題を起こすので、より重大でありよく検討する必要がある、ということ。）
Chapter 5: Revolt into Pluralism, n.3 Let us now consider more closely the meaning of the axiom of internal relations and the grounds for and against it. We have, to begin with, two possible meanings, according as it is held that every relation is really constituted by the natures of the terms or of the whole which they compose, or merely that every relation has a ground in these natures. I do not observe that idealists distinguish these two meanings ; indeed, speaking generally, they tend to identify a proposition with its consequences, thus embodying one of the distinctive tenets of pragmatism. The distinction of the two meanings is, however, less important than it would otherwise be, owing to the fact that both meanings lead, as we shall see, to the view that there are no relations at all. Source: My Philosophical Development, chap. 5：1959． More info.:https://russell-j.com/beginner/BR_MPD_05-030.HTM
私は1907年（注：添付写真は1907年の、35歳のラッセル＝髭を はやしていた時）に英国哲学会（注：the Aristotelian Society アリストテレスについて研究する学会ではない。因みに、みすず書房版の訳書で野田又夫氏は「アリストテレス学会」と訳出）で私が読み上げた論文 －それはハロルド・ヨアキムの著書『真理の本性』（The Nature of Truth)を扱ったものであった（注：ヨアヒムとの表記あり）ー の一部をここに引用することによって、この問題の重要性をおそらく最もよく例示することができると思う。 我々が今まで考察してきた学説は全て一つの論理説（論理学上の学説）から演繹可能であり、その中心的な学説は次のように言いあらわしてよいだろう。（訳注：以下は最後まで、ラッセルの考えではなく、ラッセルが攻撃しようとする一元論的観点の説明であることに注意）： (即ち)「あらゆる関係は、関係づけられた諸項の本性によって基礎づけられている。」 これを内面的関係の公理と呼ぶことにしよう。この公理からただちに、実在あるいは真理の全体はヨアキム氏の言う意味で「有意義な全体( a significant whole)」でなければならない、ということが帰結する(It follows ～ that)。というのは、個々の部分（各部分）は、他の部分の全て及び全体に対して、それのもつ関係を明示する（exhibits 開陳する）ところの性質持っているからである。従って、どれか一つの部分の本性(性質)が完全に知られているならば、全体及び他のすべての部分との本性（性質）もまたそれに完全に知られるであろう（ということになる）。逆に，全体の本性（性質）が完全に知られているならば、全体の各部分に対する関係、従ってまた、各部分が他の個々の部分に対してもつ関係、従ってまた、各部分の本性（性質）も、それに含まれていなければならない（知られていなければならない）。実在または真理がヨアキム氏のいう意味での有意義な全体であるならば、内面的関係の公理が真でなければならないということも、明白である。こうして上記の公理は、真理についての一元論的理論と等値である。 さらにまた、我々が一つの「もの」（a thing）とその「本性」(性質)とを区別すべきでないと仮定するならば、上記の公理から、いかなるものも全体への関係なしには十分に真実なやり方で考察することはできない、ということになる（という結論が出てくる）。なぜなら、「ＡはＢに関係している」ということを我々が考える場合、そのＡとＢはまた、他の全てのものに関係しているのであり、従ってＡとＢが何であるかを言うためには、宇宙における他の全てのものに言及する必要があるからである。もし我々Ａの本性のうち、それによってＡがＢに関係づけられる部分のみを考察するならば、我々はＢに関係するものとしてのＡ（A qua related to B）を考察している.と言える。けれどもこれ、Ａを考察する、抽象的なかつ部分的にのみ真な方法である。なぜなら、ＡそのものであるところのＡの本性（性質）は、Ｂに対すると共に他の全てのものに対する関係の基礎を含んでいるからである。こうして，全宇宙を考慮に入れなければ、十分な意味で真な何ごともＡについて言うことができない。そしてそうなると、Ａについて言われることは、他のいかなるものについて言われることと同じものになるであろう。それは、相異なるものの本性（性質）は、ライプニッツの単子の本性（性質）と同様に、すべて同一の「関係の体系」を表現せざるをえないからである。 （訳注：以上はこれから批判しようとしている「内的関係説」の立場の説明です!。）
Chapter 5: Revolt into Pluralism, n.2 I think perhaps I can best illustrate the importance of this question by quoting part of a paper that I read to the Aristotelian Society in 1907 , which deals with Harold Joachim’s book on The Nature of Truth. The doctrines we have been considering may all be deduced from one central logical doctrine, which may be expressed thus: ‘Every relation is grounded in the natures of the related terms.’ Let us call this the axiom of internal relations. It follows at once from this axiom that the whole of reality or of truth must be a significant whole in Mr Joachim’s sense. For each part will have a nature which exhibits its relations to every other part and to the whole; hence, if the nature of any one part were completely known, the nature of the whole and of every other part would also be completely known; while conversely, if the nature of the whole were completely known, that would involve knowledge of its relations to each part, and therefore of the relations of each part to each other part, and therefore of the nature of each part. It is also evident that, if reality or truth is a significant whole in Mr Joachim’s sense, the axiom of internal relations must be true. Hence the axiom is equivalent to the monistic theory of truth. Further, assuming that we are not to distinguish between a thing and its ‘nature’, it follows from the axiom that nothing can be considered quite truly except in relation to the whole. For if we consider ‘A is related to B’, the A and the B are also related to everything else, and to say what the A and the B are would involve referring to everything else in the universe. When we consider merely that part of A’s nature in virtue of which A is related to B, we are said to be considering A qua related to B; but this is an abstract and only partially true way of considering A, for A’s nature, which is the same thing as A, contains the grounds of its relations to everything else as well as to B. Thus nothing quite true can be said about A short of taking account of the whole universe; and then what is said about A will be the same as what would be said about anything else, since the natures of different things must, like those of Leibniz’s monads, all express the same system of relations. Source: My Philosophical Development, chap. 5：1959． More info.:https://russell-j.com/beginner/BR_MPD_05-020.HTM
G. E. ムーアと私がカント及びヘーゲルに反抗したのは（反対するようになったのは）,1898年の終り頃（注：ラッセル26歳の時）であった。先陣を切ったのはムーアであるが、私も彼の歩みに密接して追従した。新しい哲学の最初に発表したレポート（報告）は、雑誌「マインド」に掲載されたムーアの論文「判断の本性」であったと思う。ムーアも私も今ではこの論文の所説の全てに固守しようとは思わないが、私は －そしてムーアもそうだと思うが－ 今でもその論文の否定的な部分には同意したい。即ち、一般的に言って，事実は経験からは独立したものであるという主張である。我々二人は意見が一致してはいたが、新しい哲学のどの点に最も強い関心を抱いているかという点では異なっていた，と思う。ムーアは観念論をしりぞけることに最も関心をもっていたと思うが、私は何よりも一元論をしりぞけることに最も関心を持っていた。けれども，この二つのことは密接に関連しており,それらは、F. H. ブラッドリ（1846-1924、イギリスの観念論哲学者で,主著は『現象と実在（1893年））がヘーゲルの哲学から（精製して）とり出した（ところの）,関係についての学説によって繋がっていた（結び付けられていた）。私はそれを「内面的関係説」と呼び、私自身の説を「外面的関係説」と呼んだ。「内面的関係説」というのは.２つの項（terms）の間のあらゆる関係は,第一義的には２つの項がそれぞれに持つ本質的な（固有の）特性であり、そうして（しかも/かつ）究極においてはその２つの項が構成する全体の持つ特性である、という主張（説）である。ある種の関係については、この見方はもっともらしく見える（plausible）。たとえば,愛あるいは憎しみをとってみよう。もしＡがＢを愛する（愛している）ならば、この関係は、その関係自体を例示しており、Ａのある精神状態で成り立っていると言ってもよいだろう。無神論者でさえ、人は神を愛することが可能であることを認めなければならない（認めないわけにはいかない）。そうして、神を愛することは、愛を感ずる者の精神状態（心的状態）であり、厳密に言えば、一つの関係的事実ではない、ということになる（注：対象がどうであれ、おかしな精神状態になり、おかしな対象に愛を感ずることもありうる）。しかし，私が興味をもった関係はもっと抽象的な種類の関係であった。（即ち）たとえば，ＡとＢは事象（出来事）であり、事象Ａが事象Ｂより先に起ったと仮定してみよう。このことが、Ａの中に、Ｂとは独立に、Ａをしてある特性 ー－我々はＢに言及することによってその特性を不正確に言い表わす－－ を持たせなければならない（必然的に持たせる）何らかのものがあるということを意味する,とは私は考えない。ライプニッツは（これについて）極端な例をあげている。（即ち）彼曰く：ヨーロッパに住んでいるある男がインドに一人の妻を持っていて、その妻が夫の知らないうちに死ぬとしたならば、その男は妻の死の瞬間に（妻が死ぬやいなや）本質的な変化(intrinsic change)を蒙むることになる、と。これが 私が（当時）戦っていた説（学説）である。私はこういう内面的関係説が、特に「非対称的関係」（asymmetrical）－－もしたとえＡがＢに対しては成り立つとしても、ＢはＡに対しては成り立たない,ような関係（if = even if）－－ の場合にはあてはまらないということを発見した。(その非対称的関係の例として)「先立つ（earlier）」という関係をとりあげてみよう。ＡがＢに先立つならば、ＢはＡに先立つことはない。この時、ＡのＢに対する関係を、（内面的関係説に従って）ＡとＢについての（修飾する）形容詞によって言い表わそうとするならば、我々は日付によってそれを試みなければならない（試みるよりほかない）であろう。即ち、Ａの日付はＡの特性であり、Ｂの日付はＢの特性である、と我々は言ってよいかも知れない。しかしそれではあなたの助けにならない（何にもならない）。なぜなら、我々はさらに続けて、Ａの日付がＢの日付「より先」であると言わならず、そうして「より先」という関係から依然として脱出することができないからである。もしこの関係をＡとＢとから成る全体の特性（注：一元論的観点）と見ようと企てるならば、我々はもっとひどい困難に落ちこむことになる。なぜなら、そういう全体の中では、ＡとＢとは順序をもたず、従って「ＡがＢに先立つ」と「ＢがＡに先立つ」とを区別することができないからである。非対称的関係は、数学の大部分の部門において欠くべからざるものであるので、この説（内面的関係説）は重大であった（のである）。（注：内面的関係説は捨てなければならない，ということ)
Chapter 5: Revolt into Pluralism, n.1 It was towards the end of 1898 that Moore and I rebelled against both Kant and Hegel. Moore led the way, but I followed closely in his footsteps. I think that the first published account of the new philosophy was Moore’s article in Mind on ‘The Nature of Judgement’. Although neither he nor I would now adhere to all the doctrines in this article, I, and I think he, would still agree with its negative part — i.e. with the doctrine that fact is in general independent of experience. Although we were in agreement, I think that we differed as to what most interested us in our new philosophy. I think that Moore was most concerned with the rejection of idealism, while I was most interested in the rejection of monism. The two were, however, closely connected. They were connected through the doctrine as to relations, which Bradley had distilled out of the philosophy of Hegel. I called this ‘the doctrine of internal relations’, and I called my view ‘the doctrine of external relations’. The doctrine of internal relations held that every relation between two terms expresses, primarily, intrinsic properties of the two terms and, in ultimate analysis, a property of the whole which the two compose. With some relations this view is plausible. Take, for example, love or hate. If A loves B, this relation exemplifies itself and may be said to consist in certain states of mind of A. Even an atheist must admit that a man can love God. It follows that love of God is a state of the man who feels it, and not properly a relational fact. But the relations that interested me were of a more abstract sort. Suppose that A and B are events, and A is earlier than B. I do not think that this implies anything in A in virtue of which, independently of B, it must have a character which we inaccurately express by mentioning B. Leibniz gives an extreme example. He says that, if a man living in Europe has a wife in India and the wife dies without his knowing it, the man undergoes an intrinsic change at the moment of her death. This is the kind of doctrine that I was combating. I found the doctrine of internal relations particularly inapplicable in the case of ‘asymmetrical’ relations — i.e. relations which, if they hold between A and B, do not hold between B and A. Let us take again the relation earlier. If A is earlier than B, then B is not earlier than A. If you try to express the relation of A to B by means of adjectives of A and B, you will have to make the attempt by means of dates. You may say that the date of A is a property of A and the date of B is a property of B, but that will not help you because you will have to go on to say that the date of A is earlier than the date of B, so that you will have found no escape from the relation. If you adopt the plan of regarding the relation as a property of the whole composed of A and B, you are in a still worse predicament, for in that whole A and B have no order and therefore you cannot distinguish between ‘A is earlier than B’ and ‘B is earlier than A’. As asymmetrical relations are essential in most parts of mathematics, this doctrine was important. Source: My Philosophical Development, chap. 5：1959． More info.:https://russell-j.com/beginner/BR_MPD_05-010.HTM
空間と時間とを最初から含めておくことによって、純粋論理の弁証法よりももっと密接な関係を「現象」（Appearance 大文字であることに注意）に対して持つところの弁証法を、また、単なるカテゴリー（範疇）の図式化/体系化以上のものによって，そこから多分異なった（別の）弁証法を，獲得できると思われる（訳注：論理学は通常、時間や空間は関係ない，またそういったものを捨象しないといけない、と考えられている）。というのは，カテゴリー（範噂）と感覚との間には化学的結合ともいってよいようなものがあって、純粋なカテゴリー（範噂）を後から図式化/体系化するだけでは得られないような新たな観念を生むかも知れないからである。この弁証法において（は）、量（というもの）は直接的な所与（データ）そのものにのみ適用可能な概念であるという（前に得られた）結果から、しかもその適用によって直接的な所与（データ）を媒介されたものにする概念であるという結果から、私は始めるべきであろう。従って、量から弁証法的に派生する全てのものは、論理的な範噂（カテゴリー） －それらの論理的範疇はいずれも接着力としての（as stick）直接的所与（データ）そのものにはまったく適用されない－ とは根本的に（materially）異なるものであろう。この見解は，数学の成功を支持するとともに、数学の成功を説明するものである。この見解に従えば、連続体とか充実体(pulenum プレナム：物質が充満した空間 )とかいうような観念において、論理学によっては求めても得られない直接性が、保持されるということが可能（＝保持されうる）と思われる。このようにして、我々は、まず「実在」を構成し,次に「実在」と「現象」とのどうにもならない二元性に直面させられるというやり方ではなく、まず「現象」から出発してそれを「実在」に変える方法を見つけ出すことが可能となるであろう。 しかし、そのような弁証法においては、最後の段階を除いた全ての段階において、無矛盾性（self-consistency 首尾一貫性）をあまりも厳しく要求することは避けなければならない,ということは守られるべきである（to be observed that 順守されるべき）。感覚的要素が常に存在するはずであるから（is to be present 現前する運命にある）、我々の概念が矛盾をふくむ場合でも、その全ての矛盾を我々の概念を非難するものと見なすことはできない。（即ち）矛盾のあるものは、感覚的要素から不可避的に生ずるものと見なさなければならない。それゆえ,そのような弁証法を構成するに先立って、避けうる矛盾と不可避的矛盾とを区別するための原理が発見されなければならない。私の考えでは、唯一の不可避の矛盾（と）は,量に属する矛盾である。即ち、「二つの物は、概念的にはあらゆる点において同一でありながら、異なったものでありうる」ということと、それにもかかわらず「そういう相違（注：量における相違）はやはりひとつの概念でありうる」ということとの間の矛盾である（量に関する矛盾）。この矛盾の必然性は、相違が感覚において与えられうるという事実に由来していると思われる。
Chapter 4: Excursion into Idealism, n.9 On re-reading what I wrote about the philosophy of physics in the years 1896 to 1898, it seems to me complete nonsense, and I find it hard to imagine how I can ever have thought otherwise. Fortunately, before any of this work had reached a stage where I thought it fit for publication, I changed my whole philosophy and proceeded to forget all that I had done during those two years. The notes I made at that time have, however, a possible historical interest, and, although they now seem to me to be misguided, I do not think that they are any more so than the writings of Hegel. Some of the more salient passages from the notes that I made in those years follow. On the Idea of a Dialectic of the Sciences (January 1, 1898) It seems possible, by including space and time from the beginning, to obtain a dialectic having a closer relation to Appearance than that of pure Logic, and perhaps differing therefrom by more than the mere schematization of categories. For there may be what we might call a chemical union between categories and sense, leading to new ideas not obtainable by mere subsequent schematization of pure categories. In this dialectic, I should start from the result that quantity is a conception applicable only to immediate data as such, and yet rendering them mediate by its application. Everything, therefore, to be derived dialectically from quantity would differ materially from the logical categories, none of which applies to immediate data as stick. The success of mathematics both sustains and is explained by the present view. It seems possible that, in such ideas as the continuum and the plenum, the immediacy vainly sought by logic is retained. We might thus find a method of turning Appearance into Reality, instead of first constructing Reality and then being confronted by a hopeless dualism. But it is to be observed that, in such a dialectic, one must avoid, at all stages short of the last, too rigid a demand for self-consistency. Since a sensuous element is to be always present, we cannot regard every contradiction as condemning our conceptions ; some must be regarded as inevitably resulting from the sensuous element. Before such a dialectic can be constructed, therefore, a principle must be discovered by which to distinguish avoidable from unavoidable contradictions. I believe the only unavoidable contradiction will be that belonging to quantity, namely that two things may differ though in all points conceptually identical, and that the difference may be a conception. This contradiction appears to derive its necessity from the fact that differences may be given in sense. Source: My Philosophical Development, chap. 4,1959． More info.:https://russell-j.com/beginner/BR_MPD_04-090.HTM
私が関心をもったもう一つの問題は、物質が空虚な空間によって切り離されている諸原子から成っているのか、それとも全空間（全宇宙）に広がるプレナム（注：”plenum”：物質が充満した空間）から成っているのか、という問題であった。当初，私は前者の見方に傾いていた。（注：現代物理学・宇宙論においても、宇宙において物質が占める割合はごくわずかであり、大部分はダーク・マターやダーク・エネルギーで占められていると主張されている。）この見方を最も論理的に述べた主唱者（exponent）はボスコヴィッチ（Boscovitch）であった。彼の見解によれば，一つの原子は空間の一点のみを占めるのであり、また（かつ）あらゆる（物質間の）相互作用は、ニュートンの万有引力の法則においてそうであるように、遠隔作用である。けれども，これとは異なる見解がファラデーの実験から生れており、電気と磁気に関するクラーク・マックスウェルの大著に具体的に示されていた。この著作はホワイトヘッドの給費研究員資格請求論文の主題となっていた。(原注：この理由により，ホワイトヘッドはケンブリッジでは，常に，純粋数学者であるよりもむしろ応用数学者であると見なされた。この見方は、ホワイトヘッドが『普遍的代数学』を書いたにも代わらず，『普遍的代数学』はそれが受けるに値するだけの注目をケンブリッジ大学は払わなかった。) 彼は私にボスコヴィッチの見方（見解）を捨ててこの見方（見解）をとるようにしきりに勧めた。この見解は、それを支持する経験的議論（論拠）をもっている上に、遠隔作用をなくす(仮定しなくてもよい)という長所も持っていた。遠隔作用は長い間、ニュートン自身にとってすらも、信じがたいものと思われていたものであった。より現代的なこの見方を採用した時、私はそれにヘーゲル風の衣裳をまとわせ、それをライプニッツからスピノザへの弁証法的移行として示し、そうして私が論理的順序と考えるものを、年代記の順序（時間順）に優先することを思い切って許したのである（注：年代の上ではスピノザの方がライプニッツより先／permit myself to allow）
Chapter 4: Excursion into Idealism, n.8 The other problem which concerned me was the question whether matter consists of atoms separated by empty space, or of a plenum pervading all space. I inclined at first to the former view, of which the most logical exponent was Boscovitch. According to his view, an atom occupies only a point of space, and all interaction is action at a distance, as in the Newtonian law of gravitation. A different view, however, had resulted from Faraday’s experiments and been embodied in Clerk Maxwell’s great book on electricity and magnetism. This book had been the subject of Whitehead’s Fellowship dissertation (* note), and Whitehead urged me to prefer its views to those of Boscovitch. In addition to empirical arguments in its favour, it had the advantage of doing away with action at a distance, which had always seemed incredible, even to Newton. When I adopted the more modern view, I gave it a Hegelian dress, and represented it as a dialectical transition from Leibniz to Spinoza, thus permitting myself to allow what I considered the logical order to prevail over that of chronology. (* Note: On this ground, Whitehead was always regarded at Cambridge as an applied, rather than a pure, mathematician. This view persisted in spite of Universal Algebra, to which Cambridge paid much less attention than it deserved. Source: My Philosophical Development, chap. 4,1959． More info.:https://russell-j.com/beginner/BR_MPD_04-080.HTM
Chapter 4: Excursion into Idealism, n.7 Two questions specially interested me in the philosophy of physics. The first of these was the question of absolute or relative motion. Newton had an argument to show that rotation must be absolute and not relative. But, although this argument worried people and they could not find an answer to it, the arguments for the contrary view, that all motion is relative, seemed at least equally convincing. This puzzle remained unsolved until Einstein produced his Theory of Relativity. From the point of view of Hegelian dialectics it was a convenient source of antinomies; it was not necessary (so I supposed) to find a solution within physics, but to acknowledge that matter is an unreal abstraction and that no science of matter can be logically satisfactory. Source: My Philosophical Development, chap. 4,1959． More info.:https://russell-j.com/beginner/BR_MPD_04-070.HTM
Chapter 4: Excursion into Idealism, n.6 I had when I was younger — perhaps I still have — an almost unbelievable optimism as to the finality of my own theories. I finished my book on the foundations of geometry in 1896, and proceeded at once to what I intended as a similar treatment of the foundations of physics, being under the impression that problems concerning geometry had been disposed of. I worked on the foundations of physics for two years, but the only thing that I published expressing my views at that time was the article on number and quantity already mentioned. I was at this time a full-fledged Hegelian, and I aimed at constructing a complete dialectic of the sciences, which should end up with the proof that all reality is mental. I accepted the Hegelian view that none of the sciences is quite true, since all depend upon some abstraction, and every abstraction leads, sooner or later, to contradictions. Wherever Kant and Hegel were in conflict, I sided with Hegel. I was much impressed by Kant’s Metaphysische Anfangsgrunde der Naturwissenschaft and made elaborate notes on it, but I remarked, ‘the book is divided into four sections corresponding to the Table of Categories, and in each section three laws are found for the three corresponding categories. But the three laws are usually very artificial; two would be natural.’ Source: My Philosophical Development, chap. 4,1959． More info.:https://russell-j.com/beginner/BR_MPD_04-060.HTM
「私はこの論文で数理哲学における最も根本的な問題の一つを論じたい。微積分学（infinitesimal calculus）及びそのすべての帰結についての,要するに,高等数学全体についての,我々の解釈は、この関係（注：数と量との関係）について我々がいかなる見解を採るかに，依存していると言わなければならない。まさに連続の観念も －－ この観念は数学におけると同様哲学においても次第に人目を引くようになってきたものであり、特に近年、ヒユームとカントがともに持っていた原子論的見解をおしのけるにいたっている－－ 数学において数に対する量の意義が（相対的に）どの程度に認められるかにより（relative justification）、必然的に、左右されなければならない(stand or fall 成功するあるいは失敗する)と私は考える。けれども、ここでは数学的考察を行う必要はないだろう。数と量とを純粋に論理的な側面から考察することで十分であろう。私は,「量」という言葉を常に連続量と同等である（同じ意味をもつ）ものとして用いることにしよう。そしてこの論文において 連続的という語の意味を明瞭にすることに努めることにしよう。 私の議論（論証）は以下のようになるであろう。最初に私は数を論じ（数について論じ）、正の整数（positive integers）を超えて数を拡張すること（注：負の整数、少数・・・）は、(数の)単位の特性をしだいに消滅させること（gradual absorbsion しだいに吸収すること）によって起るものであること、そうして,数の拡張は数全体に関する情報をしだいに減少させることを、私は示すであろう（shall show）(注：わかりにくいが、正の整数の場合は、１個、２個というように応用できる、負の整数の場合は借金として考えることができる。しかしそうした解釈も、分数、少数、虚数・・・となっていくと、この世の中に実例がある数として考えられなくなっていく、また、数とは何かということもわかりにくくなっていく、といったところだろうか？)。次に私は、数を連続体へ適用することを論じ(注：物を分割できて初めて数えることができる／たとえて言えば被連続体である数個の角砂糖と連続体であるコップ一杯の水)、数自体は量に関してまったく情報を与えず、既存の量的単位との比較を与えるのみであることを、示す（明らかにする）ことに努めることにしよう（注：これもわかりにくいが、小さなコップの中の水については水の分子の数のようなものを数えるなら数がでてくるが、通常は、数の概念は出てこない。しかし、小さなコップの正確に３倍の大きさのコップに水が入っているとすると、両者を比較すると、１：３という数がでてくる）。従って、量は単位の分析において探求されなければならない，と思われるだろう。量とはいろいろな量（的なもの）の固有の（本質的）ひとつの特性であると仮定し（Assuming quantity to be an intrinsic property of quantities）、私は（以下）２つの仮説について論ずることにしよう。第一の仮説は、量を他のものに還元することのできないカテゴリー（範疇）と見なすものであり、第二の仮説は、量を直接的な感覚的所与（センス・データ）と見なすものである。第一の仮説を採用する時、外延量（extensive quantity 「示強量」という訳語もあるがわかりにくい）がその分割可能性(を仮定すること)によって矛盾に陥ち、本当は分割できないものであり、それゆえ内包的なものとして受け取られなければならないことがわかるであろう(intensive 論理学用語で「内包的」。「内包」とは,ある概念がもつ共通な性質のこと。性質は分割できない。内包に対する言葉は「外延」。広がりのある外延は分割可能)。しかし,内包量（intensive quantity 「示容量」という訳語もあるがわかりにくい）が、もしいろいろな内包量の固有の一特性であるとしたら、内包量もまた,それらの諸特性の単なる関係にすぎないに違いない、と思われるであろう。従って,第一の仮説、即ち、量は一つの内包的特性を示すカテゴリー（範噂）であるという仮説は、斥けられねばならないことになるであろう。さて第二の仮説、すなわち量は感覚における所与（データ）であるという仮説もまた、矛盾に導くことが見出されるであろう。それゆえ、我々は量がいろいろな量の内包的特性であるという見解を斥けざるをえないであろう。（そこで）その代わりに、我々は量を比較のカテゴリー（範噂）の一つと見なそう。量的にとり扱うことができるものの間には、量的に比較できる質的に類似のものが存在するという、外面的な（外部的な）特性（extraneous property）のうちに含まれるものを除いて、共通の特性はまったく存在しない,と我々は言おう。このことは、量のカテゴリー（範疇）を、最も広い意味での，尺度（measure）のカテゴリー（範噂）に変えることであり、こうして前の多くの困難（問題）は消滅する，と私は考える。しかし同時に、量と数との全ての関係（conexion = connection）は消滅するであろう。（つまり）量、あるいは尺度は、数とは全く独立した比較（の）概念である、と我々は言うであろう。しかし、尺度（measure）のうちに含まれる比較の種類についての議論は、以前の困難（問題）を新たな形で再び呼び戻すであろう。比較される諸項は －－もはや量的なものとは見なされないが－－ やはり、この論文の最初の部分で量そのものに属するに属していたであろうものに類似した矛盾に感染している（陥っている）ことに気づくであろう。私は、量とは現実的ならびに可能的な直接の所与（データ）の集合にのみ適用可能であり，いかなる十分に理解される物質(?)（fully understood material）には適用されないものである、と私は結論する（結論を下すことにしよう）。」
クーチェラ(Louis Couturat, 1868-1914:フランスの哲学者で論理学者)はこの論文のことを「精緻な弁証法の小さな傑作」（ce petit chef d’oeuvre de dialectique subtile）と言ってくれたが、今の私にとっては、全くとりえがないがらくたとしか思えない。
Chapter 4: Excursion into Idealism, n.5 However, there was worse to follow. My theory of geometry was mainly Kantian, but after this I plunged into efforts at Hegelian dialectic. I wrote a paper ‘On the Relations of Number and Quantity’ which is unadulterated Hegel. The gist of this paper is contained in its first two paragraphs, which are as follows: I wish in this paper to discuss one of the most fundamental questions of mathematical philosophy. On the view we take of this relation must depend our interpretation of the Infinitesimal Calculus and all its consequences — in a word, of all higher mathematics. The very idea of the continuum — an idea which, in philosophy as in mathematics, has become gradually more and more prominent, and has, of late especially, ousted the atomic views which were shared by Hume and Kant — must stand or fall, I think, with the relative justification of quantity in mathematics as against number. It will not be necessary, however, to deal with mathematical considerations here; it will be sufficient to consider number and quantity in their purely logical aspects. I shall use quantity, always, as equivalent to continuous quantity, and I shall endeavour, in the course of the paper, to make clear the meaning of the word continuous. My argument will be as follows: First, I shall discuss number, and show that its extensions beyond the positive integers result from a gradual absorption of the properties of the unit, and give a gradually diminishing information as to the whole. Then I shall discuss the application of number to continua, and shall endeavour to show that number per se gives no information as to quantity, but only comparison with an already quantitative unit. It will appear, therefore, that quantity must be sought in an analysis of the unit. Assuming quantity to be an intrinsic property of quantities, I shall discuss two hypotheses. The first regards quantity as an irreducible category, the second regards it as an immediate sense-datum. On the first hypothesis, we shall see that extensive quantities are rendered contradictory by their divisibility, and must be taken as really indivisible, and so intensive. But intensive quantity too, it will appear, must, if it be an intrinsic property of intensive quantities, be also a mere relation between them. The hypothesis that quantity is a category giving an intrinsic property will therefore have to be rejected. The hypothesis that quantity is a datum in sense will also be found to lead to contradictions. We shall be forced, therefore, to reject the view that quantity is an intrinsic property of quantities. We shall regard it, instead, as a category of comparison ; there is no common property, we shall say, among things that can be treated quantitatively, except what is involved in the extraneous property that there are other qualitatively similar things with which they can be quantitatively compared. This will turn quantity into measure, in the broadest sense, and with this, I think, our previous difficulties will cease. But at the same time, every connexion with number will cease — quantity or measure, we shall say, is a wholly independent conception of comparison. But a discussion of the kind of comparison involved in measure will bring back our previous difficulties in a new form; we shall find that the terms compared, though we no longer regard them as quantitative, are infected with contradictions similar to those which, in the first part of the paper, will have belonged to quantity itself. I shall conclude that quantity is only applicable to classes of actual and possible immediate data, and not to any fully understood material. Although Couturat described this article as ‘ce petit chef d’oeuvre de dialectique subtile’, it seems to me now nothing but unmitigated rubbish. Source: My Philosophical Development, chap. 4,1959． More info.:https://russell-j.com/beginner/BR_MPD_04-050.HTM
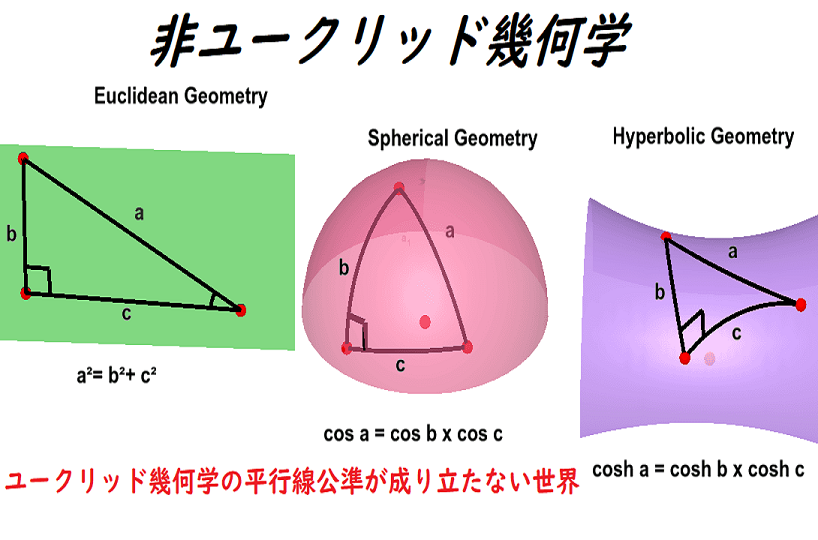
私の最初の哲学書『幾何学の基礎に関する一考察』(An Essay on the Foundations of Geometry)は、給費研究員資格請求論文に手を入れたもの（推敲したもの）であったが、今の私にとってはいくらか馬鹿げたものに思われる。私はカントの問い「いかにして幾何学は可能か」をとりあげ、空間が周知の三つの変数 －－その一つはユークリッド幾何学の、他の二つは非ユークリッド幾何学の変数であるが,不変の「曲率（measure of curvature）」を保持するという特性を持っている－－ の一つである場合にまたその場合にのみ幾何学は可能である、と結論した。アインシュタイン革命は、こういう考え方に類するものをまったく全て一掃してしまった。アインシュタインの一般相対性理論における幾何学は、私が（それ以前に）不可能だと宣言していたところのものである（あった）。アインシュタインが自説のもととしたテンソルの理論は私にも役に立ったであろうが、アインシュタインがそれを用いるまで私はそれについて聞いたことがなかった。結局、細かい点はともかくとして、この初期の自分の著書の中に何らかの妥当なものがあるとは，私は思わない。 (ウィキペディアの説明：「一般相対論において、アインシュタイン・テンソルは、エネルギーと整合性を持つような方法で、時空の曲率を記述する重力のアインシュタイン方程式の中で発生する。)
Chapter 4: Excursion into Idealism, n.4 My first philosophical book, An Essay on the Foundations of Geometry, which was an elaboration of my Fellowship dissertation, seems to me now somewhat foolish. I took up Kant’s question, ‘how is geometry possible?’ and decided that it was possible if, and only if, space was of one of the three recognized varieties, one of them Euclidean, the other two non-Euclidean but having the property of preserving a constant ‘measure of curvature’. Einstein’s revolution swept away everything at all resembling this point of view. The geometry in Einstein’s General Theory of Relativity is such as I had declared to be impossible. The theory of tensors, upon which Einstein based himself, would have been useful to me, but I never heard of it until he used it. Apart from details, I do not think that there is anything valid in this early book. Source: My Philosophical Development, chap. 4,1959． More info.:https://russell-j.com/beginner/BR_MPD_04-040.HTM
優等生試験の後,大学での次の学究上のステップは、給費研究員資格請求学位論文（a Fellowship dissertation）を執筆することであった。私は学位論文の主題として「幾何学の基礎」を選び、非ユークリッド幾何学がカントの超越論的芸術哲学（transcendental aesthetic 超越論的美学）に及ぼす影響について特に注意を払った。この学位論文の執筆作業は（work）は、経済学及びドイツ社会主義に関する執筆作業（work 研究活動）－－ の間に点在させられており（散りばめられており）、それはベルリンに二冬（ふたふゆ）を本拠地を置いて（based upon）、私の最初の著作（公刊したもの）の主題となった。ベルリンでのこの二冬、それから、その翌年（1896年）に妻と一緒のアメリカ旅行は、ケンブリッジ（大学）の偏狭さ（parochialism 地方根性）を治すのに大いに役立ち、また、私がそれ以前に聞いたことのなかったドイツ人の純粋数学に関する著作（及び研究）に気づかせた。それ以前の誓い（注：もう数学の本なんて読まない！という誓い）にもかかわらず、（誓いの後）私は大量の数学書を読んでいた。その多くは、後にわかったことであるが、私の主要な目的には全く無関係なものであった。私はダルブーの『曲面論』（Theory of Surfaces）やディニの『実変数関数論』（Theory of Functions of a Real Variable）や、フランス人の著になる数種の『解析概論』（Cours d’Analyse）や、ガウスの『一般曲面論』（General Theory of Curved Surfaces）やグラスマンの『線形延長論延長論』（Ausdehnungslehre）を読んだ。このグラスマンの本は,ホワイトヘッドによって導かれたものである。ホワイトヘッドの『普遍的代数論』(Universal Algebra)は私を大いに興奮させたが、その本はその後（ラッセル夫妻訪米時以後）すぐに出版されており（注：『普遍的代数論』は1898年に出版）、グラスマンの体系に大いに関連していた。けれども,私は、応用数学の方が純粋数学よりも価値のある研究であると（当時）信じていた。なぜなら，応用数学の方が －－私はヴィクトリア王朝時代の楽観主義でそう考えていたのだが－－ 人間の幸福をより増進しそうだからであった。私はクラーク・マックスウェル(著)『電気と磁気』を注意深く読み、ヘルツの『力学原理』を研究し、ヘルツが電磁波を作り出すことに成功したときは大いに喜んだ。J. J. トムソンの実験的研究は、大いに私の興味をひいた。私はまた、自分の目的により関連することが（後で）わかった著作、たとえば、デデキントやカントールやフレーゲの著作 －－（学位論文執筆において）私のより助けになった可能性があったが－－ は後になって（学位論文執筆後に）知ったのである。
Chapter 4: Excursion into Idealism, n.3 After the Tripos, the next academic step was the writing of a Fellowship dissertation. I chose for my subject ‘The Foundations of Geometry’ , and paid special attention to the effect of non-Euclidean geometry on Kant’s transcendental aesthetic. My work on this dissertation was interspersed with work on economics and on German social democracy, which was the subject of my first book, based upon two winters in Berlin. These two winters, and a journey to America with my wife in the following year (1896), did much to cure me of Cambridge parochialism, and made me aware of German work in pure mathematics which I had not previously heard of. In spite of my earlier vow, I read a very great deal of mathematics – much of it, as I afterwards discovered, quite irrelevant to my main purpose. I read Darboux’s Theory of Surfaces, Dini’s Theory of Functions of a Real Variable, and several French Cours d’Analyse, Gauss’s General Theory of Curved Surfaces, and Grassman’s Ausdehnungslehre, to which I was led by Whitehead, whose Universal Algebra, which greatly excited me, was published shortly after this time and was largely concerned with Grassman’s system. I was, however, persuaded that applied mathematics is a worthier study than pure mathematics, because applied mathematics – so, in my Victorian optimism, I supposed – was more likely to further human welfare. I read Clerk Maxwell’s Electricity and Magnetism carefully, I studied Hertz’s Principles of Mechanics, and I was delighted when Hertz succeeded in manufacturing electro-magnetic waves. J. J. Thompson’s experimental work interested me greatly. I read, also, works that proved more relevant to my purpose, such as those of Dedekind and Cantor, Frege, who might have helped me more, I did not know of until later. Source: My Philosophical Development, chap. 4,1959． More info.:https://russell-j.com/beginner/BR_MPD_04-030.HTM
