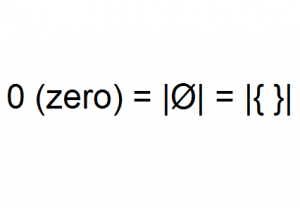 「空集合」に関して,また一般的にいって「無」の概念に関して,非常に大きな困難がある。「無」のような概念が存在すること,また,ある意味で「無」は何かあるものであることは,明白である。事実,「無は無(存在しないもの)ではない」という命題は,疑いもなく,それを真とする解釈が可能であり,その解釈はプラトンの『ソフィスト』で議論された矛盾を生ずる。記号論理学においては,「空集合」とはまったく項を含まない集合である(のことをいう)。また,記号論的には(記号論理学においては?),そういったような観念を導入することは是非必要である。(そうして)我々は,当然のごとく生ずる矛盾を避ける事ができるかどうか,よく検討しなければならない。
「空集合」に関して,また一般的にいって「無」の概念に関して,非常に大きな困難がある。「無」のような概念が存在すること,また,ある意味で「無」は何かあるものであることは,明白である。事実,「無は無(存在しないもの)ではない」という命題は,疑いもなく,それを真とする解釈が可能であり,その解釈はプラトンの『ソフィスト』で議論された矛盾を生ずる。記号論理学においては,「空集合」とはまったく項を含まない集合である(のことをいう)。また,記号論的には(記号論理学においては?),そういったような観念を導入することは是非必要である。(そうして)我々は,当然のごとく生ずる矛盾を避ける事ができるかどうか,よく検討しなければならない。
 Great difficulties are associated with the null-class, and generally with the idea of nothing. It is plain that there is such a concept as nothing, and that in some sense nothing is something. In fact, the proposition nothing is not nothing is undoubtedly capable of an interpretation which makes it true—a point which gives rise to the contradictions discussed in Plato’s Sophist. In Symbolic Logic the null-class is the class which has no terms at all; and symbolically it is quite necessary to introduce some such notion. We have to consider whether the contradictions which naturally arise can be avoided.
Great difficulties are associated with the null-class, and generally with the idea of nothing. It is plain that there is such a concept as nothing, and that in some sense nothing is something. In fact, the proposition nothing is not nothing is undoubtedly capable of an interpretation which makes it true—a point which gives rise to the contradictions discussed in Plato’s Sophist. In Symbolic Logic the null-class is the class which has no terms at all; and symbolically it is quite necessary to introduce some such notion. We have to consider whether the contradictions which naturally arise can be avoided.
出典: The Principles of Mathematics, 1903, Chap. VI. Classes: §73]
詳細情報:http://fair-use.org/bertrand-russell/the-principles-of-mathematics/s73
[寸言]
集合論において「空集合」を認める(仮定する)ことによって、数の定義が容易になる。即ち、「ゼロ」というのは、「空集合」(要素をひとつも含まない集合)であり、「ゼロ」の後者を「1」(要素をひとつだけ含む集合の集合)とすれば、「2」は(要素を2つ含む集合の集合)として定義できる。即ち「n」は(要素をn個含む集合の集合)ということになり、全ての自然数を定義できる。
