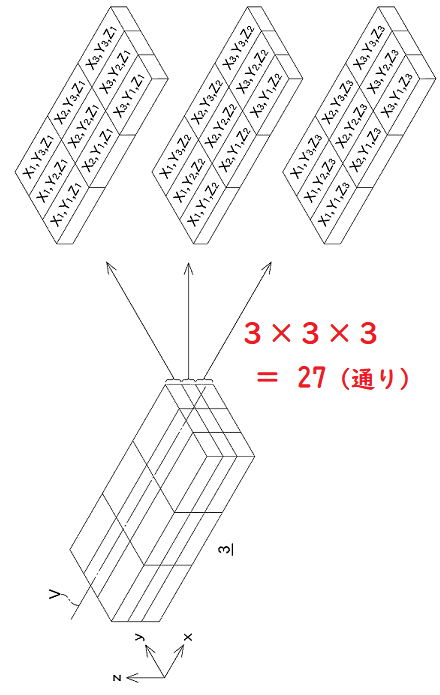
順序数(Ordinal numbers )は関係数の(一つの)部分集合(a sub-class)である。即ち，「整列された」系列(‘well-ordered’ series)の関係数である。「整列された」系列とは、その部分集合（注：ただし空集合を除く）が全て第一項(初項)を持つ系列である。超限順序数(Transfinite ordinal numbers)はカントールによって研究されたが、関係数一般は、私の知る限り、(ラッセルとホワイトヘッドの)『プリンキピア・マテマティカ』においてはじめて定義され研究された。（訳注：「無限」は「無限」であって一種類しかないと思ってしまいがちであるが、カントールは無限には種類がある（「濃度」が異なっているいろいろな無限がある）ことを発見し、それを超限数と名付けた。超限数は aleph （アレフ）の記号を用いて表記され（注：テキストでは表示できません！）、最も濃度が小さいものはアレフ・ヌル、またはアレフ・ゼロで表される。） 　一つか二つ例をあげると理解に役立つであろう。たとえば,対(つい/カップル)の系列があるとしてそれらの対から、選択の公理に関連して前述したのと同じ意味における,(新たな)選択の系列を作ろうとしているとしてみよう。そのやり方(procedure 手続き)は基数の算術（cardinal arithmetic）におけるやり方（手続き）とよく似たものであり、違っているのは（except that）、以前は選択（したもの）を集合として関心をもっていただけであったが、今度は選択（したもの）をある順序に並べることに関心をもっているということだけである。そこで再び、さきの選択したもの集合を検討する時にやったように、三つの集合（x1, x2, x3) (y1, y2, y3) (z1, z2, z3)があるとして、これらのものから選択したものでひとつの系列を作りたいと望んでいる、と想定しよう。このやり方にはいろいろある（多様な方法でやることができる）。多分、その最も単純なやり方（手順）は次のやり方であろう。（即ち）x1を含む選択は、x1を含まないものより先にくる（comes before 先立つ）。そして,二つの選択のなかで（二回選択行為をした時に）、そのどちらの選択でもx1を含む場合もｘ1を含まない場合も，y1を含むものが、y1を含まないものよりも先に置かれる（先立つ）。(次に）二つ選択したもののなかで、いずれもx1とy1とを含むかいずれもx1とy1とを含まない場合には、z1を含む選択が、z1を含まない選択より先に置かれる。同様の規則を、x2，y2，z2，についても、、x3，y3，z3についてもたてることにする、このようにすれば、あらゆる可能な選択が、x1，y1，z1ではじまり、x3，y3，z3で終わる系列に並べることができる。この系列が27の項をもつことは明らかである（注：３×３＝２９）。しかしこの場合27という数はもはや以前の例におけるように基数ではなく、順序数すなわち特別な種類の関係数である。順序数は基数と異なるのは、順序数が選択の間に順序を定めることよってであり、基数の方はそういうことしない。我々が有限数だけを考えている限り、順序数と基数との間に重要な形式的相違は存在しない。しかし、無限数を考慮に入れると、交換法則が成立しなくなるために、両者の相違は重要なものとなる。

Chapter 8 Principia Mathematica: Mathematical Aspects, n.16 Ordinal numbers are a sub-class of relation-numbers, namely, those that apply to ‘well-ordered’ series, ‘well-ordered’ series being those series in which any sub-class that has members has a first term. Transfinite ordinal numbers were studied by Cantor, but relation-numbers in general were, so far as I know, first defined and studied in the Principia. One or two illustrations may be useful. Suppose for example, that you have a series of couples and you wish to form a series of selections from these couples in the sense explained above in connection with the axiom of selection. The procedure is much akin to that in cardinal arithmetic except that we are now concerned to put the selections in an order, whereas before we were only concerned with them as a class. Suppose, again, as we did in considering class-selections, we have three sets, （x1, x2, x3) (y1, y2, y3) (z1, z2, z3), and we wish to make a series out of selections of these. There are various ways in which this can be done. Perhaps the simplest is as follows: any selection containing x1 comes before any selection which does not contain it. Among selections of which both or neither contain x1, those containing y1 come before those which do not. Among selections of which both or neither contain x1 and y1 those containing come before those which do not. We make similar rules for the suffix 2 and the suffix 3 . In this way we get all the possible selections arranged in a series which begins with ( x1, y1, x1) and ends with ( x3, y1, z1). It is obvious that the series will have twenty-seven terms, but here the number twenty-seven is no longer a cardinal number, as in our earlier example, but an ordinal number – i.e. a particular kind of relation-number. It differs from a cardinal number by establishing an order among the selections, which a cardinal number does not. So long as we confine ourselves to finite numbers, there are no important formal differences between ordinal and cardinal numbers; but, when we allow infinite numbers, the differences become important, owing to the failure of the commutative law. 　
　Source: My Philosophical Development, chap. 8：1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_08-160.HTM