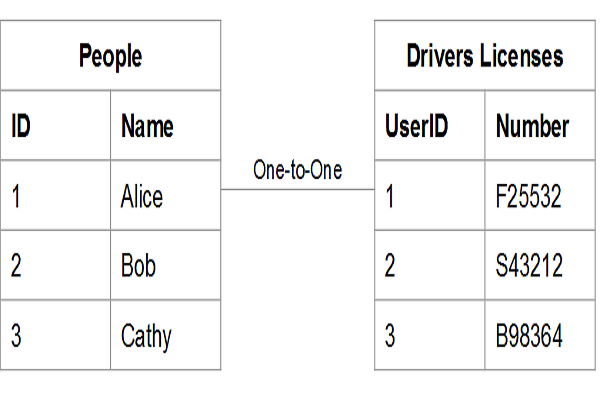
関係算術における基本的定義は、前述した「順序的類似性」（ordinal similarity）あるいは（即ち、言い換えれば）「相似性」（likeness）の定義（と同じ）である。関係に関する場合には、これ（順序的類似性）は、集合間で果たす類似性（similarity）と同様の役割を果たす。（二つの）集合間の類似性とは、一方の集合の各項を、他方の集合におけるその対応項( a correlate)と結びつける（ところの）一対一の関係が存在することである、と定義される。二つの関係PとQ（関係Pと関係Q）の間の順序的類似性とは、Pの範囲をQの範囲に対応させる一つの関係があって、二つの項がPの関係を持つ時それぞれの対応項はQの関係をもち、逆もまた真であることを意味する，と（して）定義される。実例（具体例）をあげてみよう。いまPが結婚している政府の役人たちの間の席次の上下関係(precedence)であるとし、Qは彼らの妻たちの間の席次の上下関係であるとしよう。そうすると、このとき妻の夫に対する関係は、Pの範囲とQの範囲とを対応させるものであり、妻たちがQの関係（という席次の上下関係）を相互に持つとき、彼らの夫たちはPの関係を持ち、逆もまた真である。二つの関係PとQが順序的に類似である場合、SがPとQとを対応させるところ関係（その相関関係）であるとすると、Qは、SとPとSの逆関係との関係積（the relative product ）である。たとえば,上の例で、xとyが二人の妻であり,xがyにQなる（席次の上下）関係を持つとし、かつ妻と夫との関係がSであるとすると、xは、yの夫にPなる関係をもつ一人の男の妻である。即ち、QはSとPとSの逆関係との関係積と同一なる関係である（この場合Sの逆関係とは夫の妻に対する関係(=(「妻の夫に対する関係」の逆関係))である）。PとQとが系列的関係である場合は、それらの関係の類似性は、それらの項が順序を変えることなく、相互に対応させられうる、ということを意味する。しかしこういう関係に限らず、相似性（likeness）の概念は(注：野田氏は「類似性」similarity と訳してしまっている。)、範囲をもつ全ての関係 －関係の領域と逆領域とが同じ型に属するもの－ に適用しうるものである。

Chapter 8 Principia Mathematica: Mathematical Aspects, n.14 The fundamental definition in this subject is that of ‘ordinal similarity’ or ‘likeness’, which was mentioned above. Where relations are concerned, this plays the same part as similarity played between classes. Similarity between classes is defined as the existence of a one-one relation coupling each term of either class to a correlate in the other. Ordinal similarity between two relations P and Q is defined as meaning that there is a correlator of the field of P to the field of Q which is such that whenever two terms have the relation P their correlates have the relation Q, and vice versa. Let us take an illustration: suppose P is the relation of precedence among married government officials, and Q is the relation of precedence among their wives, then the relation of wife to husband so correlates the fields of P and Q that, whenever the wives have the relation Q, their husbands have the relation P, and vice versa. When two relations P and Q are ordinally similar, if S is the correlating relation, Q is the relative product of S and P and the converse of S. In the above illustration, for example, if x and y are two wives and x has the relation Q to y, and if S is the relation of wife to husband, then x is the wife of a man who has the relation P to the husband of y, that is to say, Q is the same relation as the relative product of S and P and the converse of S; the converse of S being the relation of husband to wife. Whenever P and Q are serial relations, their likeness consists in the fact that their terms can be correlated without change of order, but the conception of likeness is applicable to all relations that have fields — i.e. to all relations where the domain and converse domain are of the same type.
　Source: My Philosophical Development, chap. 8：1959． 　
　More info.:https://russell-j.com/beginner/BR_MPD_08-140.HTM